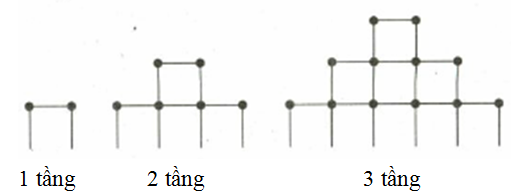
Cho dãy số vô hạn \(\left\{ {{u_n}} \right\}\)là cấp số cộng có công sai \(d\), số hạng đầu \({u_1}\). Hãy chọn khẳng định sai?
Câu hỏi trong đề: Bộ 19 đề thi Giữa kì 1 Toán 11 có đáp án !!
Quảng cáo
Trả lời:
Ta có công thức tổng \(n\)số hạng đầu tiên của cấp số cộng là: \({S_n} = n{u_1} + \frac{{n\left( {n - 1} \right)d}}{2}\)
Suy ra \({S_{12}} = 12{u_1} + \frac{{12.11.d}}{2}\)\( = 6\left( {2{u_1} + 11d} \right)\)\( \ne \frac{n}{2}\left( {2{u_1} + 11d} \right)\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Trọng tâm Sử, Địa, GD KTPL 11 cho cả 3 bộ Kết nối, Chân trời, Cánh diều VietJack - Sách 2025 ( 38.000₫ )
- Sách - Sổ tay kiến thức trọng tâm Vật lí 11 VietJack - Sách 2025 theo chương trình mới cho 2k8 ( 45.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
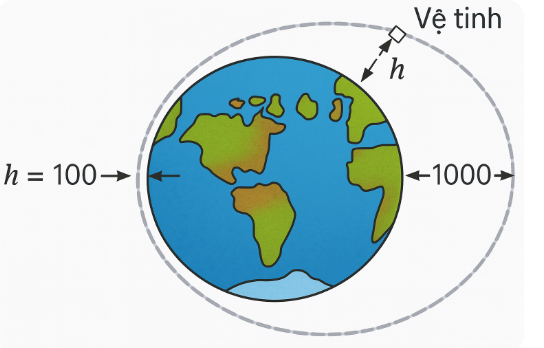
Ta có \( - 1 \le \cos \left( {\frac{\pi }{4} + \frac{{\pi t}}{{50}}} \right) \le 1 \Leftrightarrow 100 \le 550 + 450\cos \left( {\frac{\pi }{4} + \frac{{\pi t}}{{50}}} \right) \le 1000 \Leftrightarrow 100 \le h \le 1000\)
Suy ra, \(h\) đạt giá trị lớn nhất bằng \(1000\) khi \(\cos \left( {\frac{\pi }{4} + \frac{{\pi t}}{{50}}} \right) = 1 \Leftrightarrow \frac{\pi }{4} + \frac{{\pi t}}{{50}} = k2\pi \Leftrightarrow t = - 12,5 + 100k\left( {k \in \mathbb{Z}} \right)\)
Mà \(t \in \left[ {0;120} \right]\) nên \(\left\{ \begin{array}{l}0 \le - 12,5 + 100k \le 120\\k \in \mathbb{Z}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}0,125 \le k \le 1,325\\k \in \mathbb{Z}\end{array} \right. \Leftrightarrow k = 1\).
Với \(k = 1\) thì \(t = 87,5\).
Vậy thời điểm thực hiện thí nghiệm là \(87,5\) phút.
Lời giải
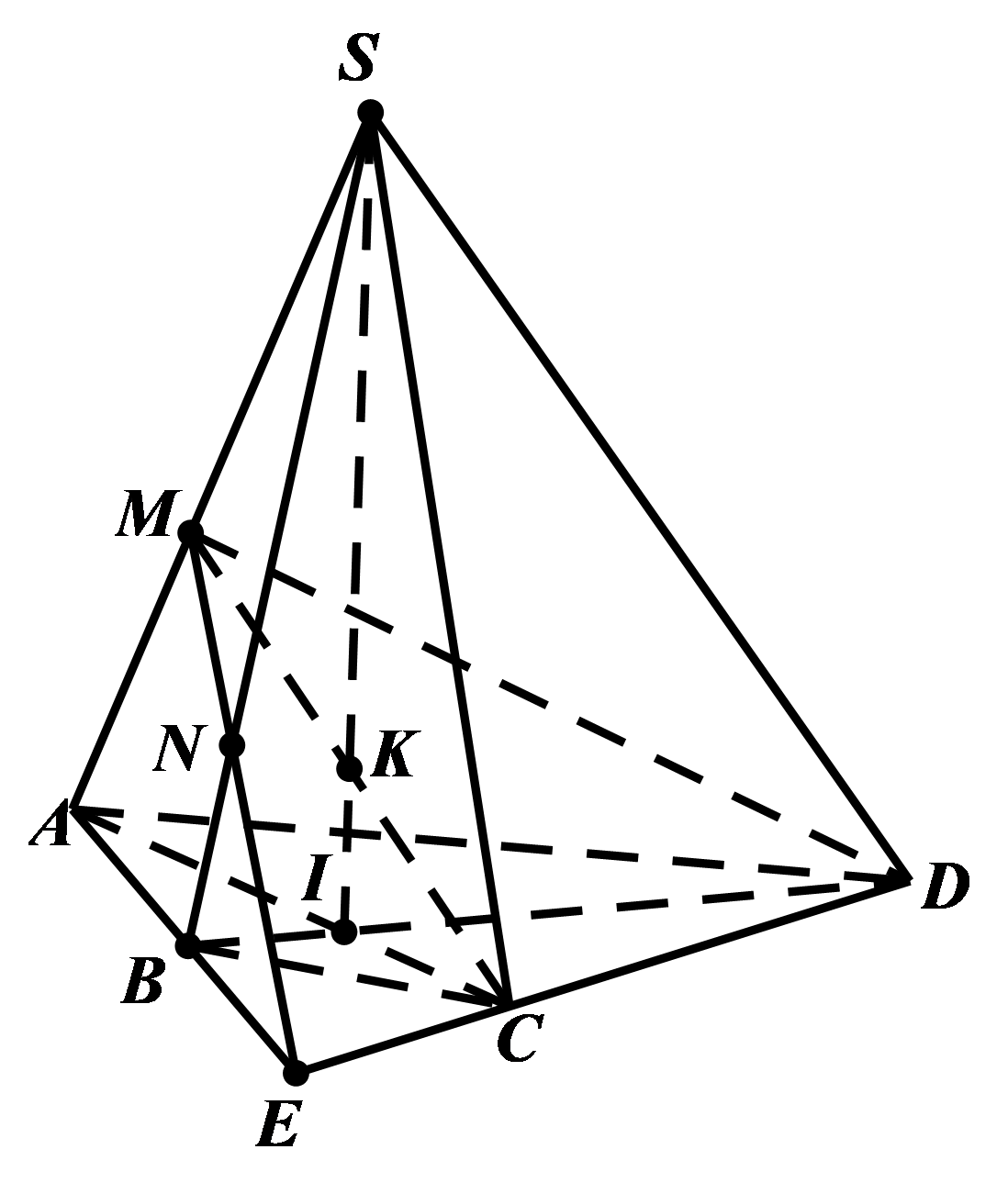
Trong \[\left( {ABCD} \right)\] gọi \[I = AC \cap BD\].
Trong \[\left( {SAC} \right)\] gọi \[K = MC \cap SI\].
Ta có \[K \in SI \subset \left( {SBD} \right)\] và \[K \in MC\] nên \[K = MC \cap \left( {SBD} \right)\].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. \(270\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.