khoahoc.vietjack.com
Giảm 50% Kích hoạt VIP
khoahoc.vietjack.com
Kích hoạt VIP Đăng nhập
Tạo VIP
  2. Lớp 11
  3. Toán

Câu hỏi:

27/10/2025 1,608 Lưu

PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 2.

Để tích lũy tiền cho việc học đại học của con gái, cô Thảo quyết định hằng tháng bỏ ra 500 nghìn đồng vào tài khoản tiết kiệm, được trả lãi \(0,5{\rm{\% }}\) cộng dồn hằng tháng. Cô bắt đầu chương trình tích luỹ này khi con gái cô tròn 4 tuổi. Cô ấy sẽ tích luỹ được bao nhiêu tiền vào thời điểm gửi khoản tiền thứ 180? Lúc này con gái cô Thảo bao nhiêu tuổi?

Xem lời giải

Câu hỏi trong đề: Bộ 19 đề thi Giữa kì 1 Toán 11 có đáp án !!

Flashcard Bắt Đầu Thi Giao bài

Quảng cáo

Trả lời:

verified Giải bởi Vietjack

Gọi \({u_n}\) là số triệu đồng mà cô Thảo có trong chương trình tích luỹ ở lần gửi thứ \(n\) (vào đầu tháng thứ \(n\)).

Kí hiệu \(a = 0,5\) triệu đồng, \(r = 0,5{\rm{\% }}\).

Số tiền của cô Thảo trong chương trình ở đầu tháng 1 là \({u_1} = a\).

Số tiền của cô Thảo trong chương trình ở đầu tháng 2 là \({u_2} = {u_1}\left( {1 + r} \right) + a\).

Số tiền của cô Thảo trong chương trình ở đầu tháng 3 là

\({u_3} = {u_2}\left( {1 + r} \right) + a = a{(1 + r)^2} + a\left( {1 + r} \right) + a{\rm{.\;}}\)

Tương tự cho các tháng tiếp theo, suy ra số tiền của cô Thảo trong chương trình ở đầu tháng \(n\) là: \({u_n} = a{\left( {1 + r} \right)^{n - 1}} + a{\left( {1 + r} \right)^{n - 2}} +  \ldots  + a\left( {1 + r} \right) + a = a\frac{{{{\left( {1 + r} \right)}^n} - 1}}{{\left( {1 + r} \right) - 1}} = a\frac{{{{\left( {1 + r} \right)}^n} - 1}}{r}{\rm{.\;}}\)

Vào thời điểm gửi khoản tiền thứ 180, cô ấy sẽ tích luỹ được \({u_{180}} = a\frac{{{{\left( {1 + r} \right)}^{180}} - 1}}{r} = 145,41\) (triệu đồng). Khi đó, tuổi của con gái cô Thảo là \(4 + 180:12 = 19\) tuổi.

Đang tải chế độ Học...

Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay

ĐẶC QUYỀN VIP

Đăng ký VIP để học và luyện thi không giới hạn

Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.

  • Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
  • Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
  • Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
  • Tải xuống đề thi [DOCX] với đầy đủ đáp án
  • Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
  • Bao gồm tất cả các bậc từ Tiểu học đến Đại học
  • Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
  • Đăng ký ngay
Avatar

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Một vệ tinh bay quanh Trái Đất theo một quỹ đạo hình Elip (như hình vẽ):

Ta có \( - 1 \le \cos \left( {\fr (ảnh 1)

Độ cao \(h\) (tính bằng kilômet) của vệ tinh so với bề mặt Trái Đất được xác định bởi công thức \(h = 550 + 450 \cdot \cos \left( {\frac{\pi }{4} + \frac{{\pi t}}{{50}}} \right)\). Trong đó \(t\) là thời gian tính bằng phút kể từ lúc vệ tinh bay vào quỹ đạo. Người ta cần thực hiện một thí nghiệm khoa học khi vệ tinh cách mặt đất xa nhất trong khoảng 120 phút đầu tiên kể từ lúc vệ tinh bay vào quỹ đạo, hãy tìm thời điểm để có thể thực hiện thí nghiệm đó? (làm tròn kết quả đến hàng phần chục theo đơn vị phút).

Lời giải

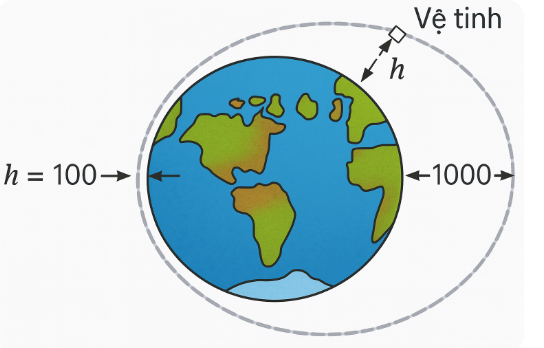
Ta có \( - 1 \le \cos \left( {\frac{\pi }{4} + \frac{{\pi t}}{{50}}} \right) \le 1 \Leftrightarrow 100 \le 550 + 450\cos \left( {\frac{\pi }{4} + \frac{{\pi t}}{{50}}} \right) \le 1000 \Leftrightarrow 100 \le h \le 1000\)

Suy ra, \(h\) đạt giá trị lớn nhất bằng \(1000\) khi \(\cos \left( {\frac{\pi }{4} + \frac{{\pi t}}{{50}}} \right) = 1 \Leftrightarrow \frac{\pi }{4} + \frac{{\pi t}}{{50}} = k2\pi  \Leftrightarrow t =  - 12,5 + 100k\left( {k \in \mathbb{Z}} \right)\)

Mà \(t \in \left[ {0;120} \right]\) nên \(\left\{ \begin{array}{l}0 \le  - 12,5 + 100k \le 120\\k \in \mathbb{Z}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}0,125 \le k \le 1,325\\k \in \mathbb{Z}\end{array} \right. \Leftrightarrow k = 1\).

Với \(k = 1\) thì \(t = 87,5\).

Vậy thời điểm thực hiện thí nghiệm là \(87,5\) phút.

Câu 2

Cho hình chóp tứ giác SABCD với đáy ABCD có các cạnh đối diện không song song với nhau và M là một điểm trên cạnh SA. Tìm giao điểm của đường thẳng MC và mặt phẳng (SBD)

Lời giải

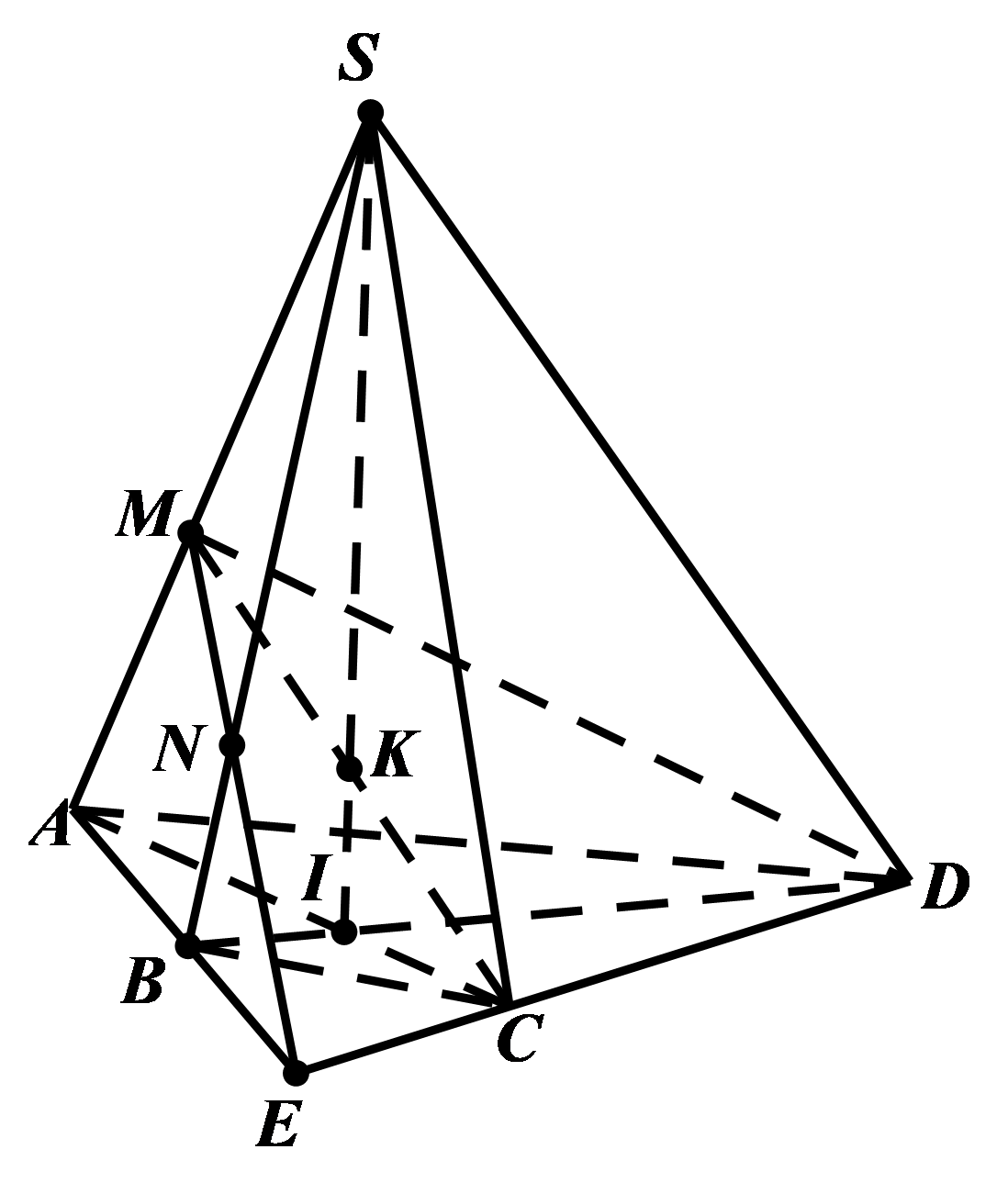
Cho hình chóp tứ giác SABCD với đáy ABCD có các cạnh đối diện không song song với nhau và M là một điểm trên cạnh SA. Tìm giao điểm của đường thẳng MC và mặt phẳng (SBD) (ảnh 1)

Trong \[\left( {ABCD} \right)\] gọi \[I = AC \cap BD\].

Trong \[\left( {SAC} \right)\] gọi \[K = MC \cap SI\].

Ta có \[K \in SI \subset \left( {SBD} \right)\] và \[K \in MC\] nên \[K = MC \cap \left( {SBD} \right)\].

Câu 3

Bạn An chơi trò chơi xếp các que diêm thành tháp theo qui tắc thể hiện như hình vẽ. Để xếp được tháp có \[10\] tầng thì bạn An cần đúng bao nhiêu que diêm?

Bạn An chơi trò chơi xếp các que diêm thành tháp theo qui tắc thể hiện như hình vẽ. Để xếp được tháp có 10 tầng thì bạn An cần đúng bao nhiêu que diêm? (ảnh 1)

A.  \(270\).                               

B.  \(100\).                  
C.  \(210\).  
D.  \(39\).

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 4

PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 2. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.

Cho lăng trụ tam giác \(ABC.A'B'C'\) có \(I\), \(K\), \(G\) lần lượt là trọng tâm các tam giác \(ABC\), \(A'B'C'\), \(ACC'\).

              a) \((ABC)\parallel \left( {A'B'C'} \right)\).   

              b) \(IG\)cắt \(\left( {BCC'B'} \right)\).

              c) \((IKG)\parallel \left( {BCC'B'} \right)\).   

              d) \(BB'\parallel \left( {ACC'A'} \right)\).

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 5

Cho dãy số vô hạn \(\left\{ {{u_n}} \right\}\)là cấp số cộng có công sai \(d\), số hạng đầu \({u_1}\). Hãy chọn khẳng định sai?              
A. \({u_n} = {u_1} + (n - 1).d\), \(\forall n \in {\mathbb{N}^*}\).                                                       
B. \({u_n} = {u_{n - 1}} + d\), \(n \ge 2\).              
C. \({S_{12}} = \frac{n}{2}\left( {2{u_1} + 11d} \right)\).                                                                       
D. \({u_5} = \frac{{{u_1} + {u_9}}}{2}\).

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 6

Cho phương trình \(\sin 2x = m\). Xét tính đúng sai của các khẳng định sau.

              a) Với \(m = 0\), phương trình có nghiệm là \(x = \frac{{k\pi }}{4}\).

              b) Phương trình có một nghiệm trên \(\left( {0;\frac{\pi }{2}} \right)\) khi \(m \in (0;1)\).

              c) Phương trình có nghiệm khi \(m \in [ - 1;1]\).

              d) Phương trình có nghiệm là \(x = \frac{\pi }{3}\) khi \(m = \frac{{\sqrt 3 }}{2}\).

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem thêm các câu hỏi khác »

Đăng ký

Bạn đã có tài khoản?

Khóa học 1 - 12
THPT
THCS
Phòng luyện đề
ĐGNL - ĐGTD
Tốt nghiệp THPT
Ôn vào 10
Ôn vào 6
Tài liệu
THPT
THCS
Tin Tuyển Sinh
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
Giấy chứng nhận ĐKKD số: 0108307822 do Sở KH & ĐT TP Hà Nội cấp lần đầu ngày 04/06/2018
© 2017 Vietjack87. All Rights Reserved.
zalo Nhắn tin Zalo Hỏi bài tập