Một chiếc ô tô được đặt trên mặt đáy dưới của một khung sắt có dạng hình hộp chữ nhật với đáy trên là hình chữ nhật \(ABCD\), mặt phẳng \(\left( {ABCD} \right)\) song song với mặt phẳng nằm ngang. Khung sắt đó được buộc vào móc \(E\) của chiếc cần cẩu sao cho các đoạn dây cáp \(EA,EB,EC,ED\) có độ dài bằng nhau và cùng tạo với mặt phẳng \(\left( {ABCD} \right)\) một góc bằng \(60^\circ \). Chiếc cần cẩu kéo khung sắt lên theo phương thẳng đứng. Tính trọng lượng (làm tròn đến đơn vị nghìn N) của chiếc xe ô tô (làm tròn đến hàng đơn vị), biết rằng các lực căng \(\overrightarrow {{F_1}} ,\overrightarrow {{F_2}} ,\overrightarrow {{F_3}} \), \(\overrightarrow {{F_4}} \) đều có cường độ là \(4700\;N\) và trọng lượng của khung sắt là \(3000\;N\).
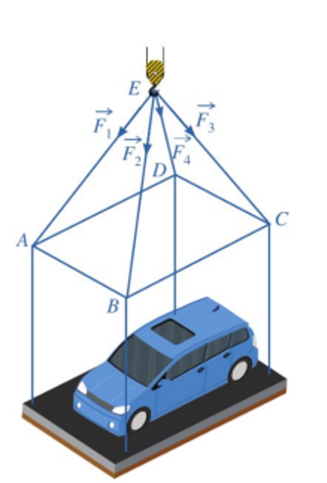
Một chiếc ô tô được đặt trên mặt đáy dưới của một khung sắt có dạng hình hộp chữ nhật với đáy trên là hình chữ nhật \(ABCD\), mặt phẳng \(\left( {ABCD} \right)\) song song với mặt phẳng nằm ngang. Khung sắt đó được buộc vào móc \(E\) của chiếc cần cẩu sao cho các đoạn dây cáp \(EA,EB,EC,ED\) có độ dài bằng nhau và cùng tạo với mặt phẳng \(\left( {ABCD} \right)\) một góc bằng \(60^\circ \). Chiếc cần cẩu kéo khung sắt lên theo phương thẳng đứng. Tính trọng lượng (làm tròn đến đơn vị nghìn N) của chiếc xe ô tô (làm tròn đến hàng đơn vị), biết rằng các lực căng \(\overrightarrow {{F_1}} ,\overrightarrow {{F_2}} ,\overrightarrow {{F_3}} \), \(\overrightarrow {{F_4}} \) đều có cường độ là \(4700\;N\) và trọng lượng của khung sắt là \(3000\;N\).

Câu hỏi trong đề: Bộ 20 đề thi Giữa kì 1 Toán 12 có đáp án !!
Quảng cáo
Trả lời:
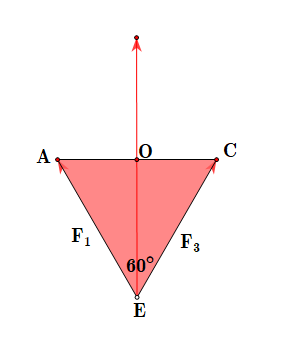
Ta có \(\widehat {AEC} = 60^\circ \)
Ta có \[\overrightarrow {{F_1}} + \overrightarrow {{F_3}} = 2\overrightarrow {EO} \Rightarrow \left| {\overrightarrow {{F_1}} + \overrightarrow {{F_3}} } \right| = 2\left| {\overrightarrow {EO} } \right| \Rightarrow \left| {\overrightarrow {{F_1}} } \right|\sqrt 3 = 4700\sqrt 3 \]
Tương tự ta cũng có \(\overrightarrow {{F_2}} + \overrightarrow {{F_4}} = \left| {\overrightarrow {{F_2}} } \right|\sqrt 3 = 4700\sqrt 3 \)
Vậy trọng lực ôtô là: \[\left( {\overrightarrow {{F_1}} + \overrightarrow {{F_2}} + \overrightarrow {{F_3}} + \overrightarrow {{F_4}} } \right) - \](trọng lực khung sắt) \( \approx 13281\left( N \right)\)
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
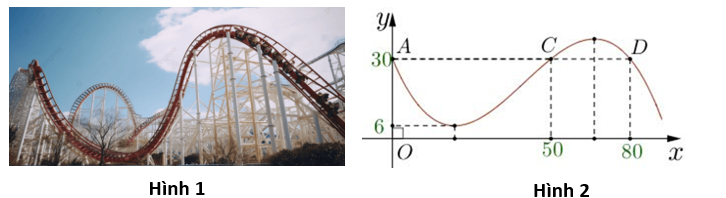
Dựa vào hình 2 ta thấy đồ thị hàm số \(y = f(x) = a{x^3} + b{x^2} + cx + d\,\,\left( {a < 0} \right)\) và đường thẳng \(y = 30\) cắt nhau tại 3 điểm phân biệt có hoành độ \(x = 0;x = 50;x = 80.\)
\( \Rightarrow a{x^3} + b{x^2} + cx + d\, = 30 \Leftrightarrow a{x^3} + b{x^2} + cx + d - 30 = 0\)có 3 nghiệm phân biệt \(x = 0;x = 50;x = 80.\)
\( \Rightarrow a{x^3} + b{x^2} + cx + d - 30 = ax\left( {x - 50} \right)\left( {x - 80} \right) = a\left( {{x^3} - 130{x^2} + 4000x} \right)\)
Suy ra \(f\left( x \right) = a\left( {{x^3} - 130{x^2} + 4000x} \right) + 30\) \( \Rightarrow f'\left( x \right) = a\left( {3{x^2} - 260x + 4000} \right)\)
\(f'\left( x \right) = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = 20\,\,\left( {TM} \right)}\\{x = \frac{{200}}{3}\,\left( {TM} \right)}\end{array}} \right.\).
Theo bài ra độ cao nhỏ nhất bằng 6 hay \(f\left( {20} \right) = 6 \Leftrightarrow a = - \frac{1}{{1500}}\)
Độ cao lớn nhất mà tàu lượn siêu tốc đạt được là \(f\left( {\frac{{200}}{3}} \right) = \frac{{3230}}{{81}} \approx 39,9.\)
Lời giải
|
a) |
Đ |
b) |
Đ |
c) |
Đ |
d) |
Đ |
(a) \(\overrightarrow {AB} = (1 - 4; - 1 - 2;2 + 1) = ( - 3; - 3;3)\)
(b) \(\overrightarrow {AB} = (1 - 4; - 1 - 2;2 + 1) = ( - 3; - 3;3) \Rightarrow |\overrightarrow {AB} | = \sqrt {{{( - 3)}^2} + {{( - 3)}^2} + {3^2}} = 3\sqrt 3 \)
(c) Gọi \(M(x;y;z)\) thì \(\overrightarrow {MC} = ( - x; - 2 - y,3 - z)\).
\({\rm{ V\`i }}\overrightarrow {AB} + \overrightarrow {CM} = \vec 0 \Rightarrow \overrightarrow {AB} = \overrightarrow {MC} \Rightarrow \left\{ {\begin{array}{*{20}{l}}{ - x = - 3}\\{ - 2 - y = - 3}\\{3 - z = 3}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x = 3}\\{y = 1}\\{z = 0}\end{array}} \right..{\rm{ }} \Rightarrow {\rm{M(3; }}1;0)} \right.{\rm{. }}\)
(d) Vì \[N\] thuộc mặt phẳng \[\left( {Oxy} \right)\] nên tọa độ điểm \[N\] là \(N(x;y;0)\)
Тa có: \(\overrightarrow {AN} (x - 4;y - 2;1);\overrightarrow {BN} (x - 1;y + 1; - 2)\)
Để \(A,B,N\) thẳng hàng thì hai vectơ \(\overrightarrow {AN} ,\overrightarrow {BN} \) cùng phương. Do đó, \(\overrightarrow {AN} = k\overrightarrow {BN} \) (với \(k\) là số thực bất kì)
Suy ra, \(\left\{ {\begin{array}{*{20}{l}}{x - 4 = k(x - 1)}\\{y - 2 = k(y + 1)}\\{1 = - 2k}\end{array} \Rightarrow \left\{ {\begin{array}{*{20}{l}}{x - 4 = - \frac{1}{2}(x - 1)}\\{y - 2 = - \frac{1}{2}(y + 1)}\\{k = \frac{{ - 1}}{2}}\end{array} \Rightarrow \left\{ {\begin{array}{*{20}{l}}{x = 3}\\{y = 1}\end{array}} \right.} \right.} \right.\). Vậy \[N\left( {3;1;0} \right)\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.