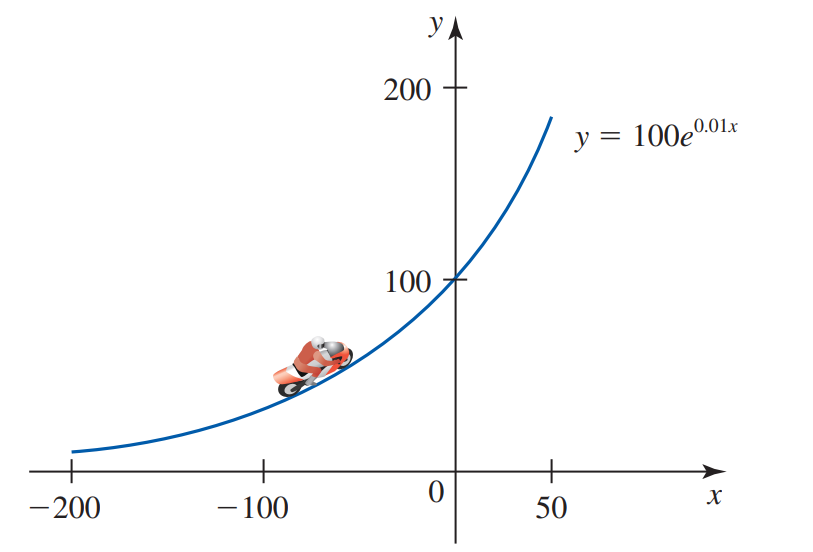
Dân số của một quốc gia sau \[t\] (năm) bắt đầu từ năm \[2023\] được tính theo công thức \[N\left( t \right) = 100{e^{0,012t}}\] (trong đó \[N\left( t \right)\] được tính bằng triệu người, \[0 \le t \le 50\])
a) Dân số của quốc gia này ở năm \[2030\] vượt mức \[110\] triệu người.
b) Dân số của quốc gia này ở năm \[2035\] vượt mức \[115\] triệu người.
c) Vào năm \[2030\] thì tốc độ tăng dân số là \[1,6\] triệu người/năm.
d) Vào năm \[2026\] thì tốc độ tăng dân số là \[1,6\] triệu người/năm.
Dân số của một quốc gia sau \[t\] (năm) bắt đầu từ năm \[2023\] được tính theo công thức \[N\left( t \right) = 100{e^{0,012t}}\] (trong đó \[N\left( t \right)\] được tính bằng triệu người, \[0 \le t \le 50\])
a) Dân số của quốc gia này ở năm \[2030\] vượt mức \[110\] triệu người.
b) Dân số của quốc gia này ở năm \[2035\] vượt mức \[115\] triệu người.
c) Vào năm \[2030\] thì tốc độ tăng dân số là \[1,6\] triệu người/năm.
d) Vào năm \[2026\] thì tốc độ tăng dân số là \[1,6\] triệu người/năm.
Câu hỏi trong đề: Bộ 20 đề thi Giữa kì 1 Toán 12 có đáp án !!
Quảng cáo
Trả lời:
|
a) |
S |
b) |
Đ |
c) |
S |
d) |
Đ |
Dân số của quốc gia này ở năm \[2030\] là \[N\left( 7 \right) = 100{e^{0,012.7}} \approx 108,8\] triệu người.Dân số của quốc gia này ở năm \[2035\] là \[N\left( {12} \right) = 100{e^{0,012.12}} \approx 115,5\] triệu người.Hàm tốc độ tăng dân số là \[N'\left( t \right) = 1,2{e^{0,012t}}\]. Ta có:
\[1,2{e^{0,012t}} = 1,6 \Leftrightarrow t \approx 2,34\].
Vậy thời vào năm \[2026\], tốc độ tăng dân số là \[1,6\] triệu người/nămHàm tốc độ tăng dân số là \[N'\left( t \right) = 1,2{e^{0,012t}}\]. Ta có:
\[1,2{e^{0,012t}} = 1,6 \Leftrightarrow t \approx 2,34\].
Vậy thời vào năm \[2026\], tốc độ tăng dân số là \[1,6\] triệu người/năm.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
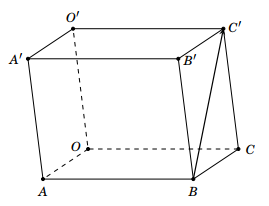
(a) Đúng: Gọi \(C'\left( {x;y;z} \right)\). Ta có \(\overrightarrow {BC'} = \left( {2; - 6;6} \right) \Rightarrow \left\{ {\begin{array}{*{20}{l}}{x - 0 = 2}\\{y - 3 = - 6}\\{z - 0 = 6}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x = 2}\\{y = - 3}\\{z = 6}\end{array}} \right.} \right.\)\( \Rightarrow C\left( {2; - 3;6} \right)\).
(b) Đúng: Gọi \(O'\left( {x;y;z} \right)\). Theo hình vẽ thì \(\overrightarrow {AO'} = \overrightarrow {BC'} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x - 1 = 2}\\{y - 1 = - 6}\\{z + 1 = 6}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x = 3}\\{y = - 5}\\{z = 5}\end{array}} \right.} \right.\)\( \Rightarrow O'\left( {3; - 5;5} \right)\)
(c) Sai: Theo hình vẽ thì \(\overrightarrow {AB'} = \overrightarrow {OC'} = \left( {2; - 3;6} \right)\).
(d) Sai: Ta có \(\overrightarrow {HK} = \overrightarrow {AB} = \left( { - 1;2;1} \right)\).
Lời giải
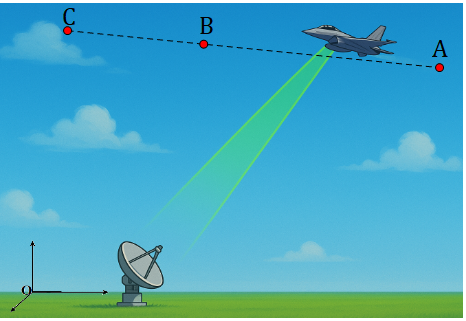
Do máy bay giữ nguyên tốc độ nên vận tốc của máy bay trên quãng đường \[AB\] và \[BC\] là như nhau. Ta có: \[\frac{{AB}}{{10}} = \frac{{BC}}{5} \Leftrightarrow AB = 2BC\].
Và máy bay giữ nguyên hướng bay nên hai vectơ \[\overrightarrow {AB} ;\,\overrightarrow {BC} \] cùng hướng.
Do đó \[\overrightarrow {AB} = 2\overrightarrow {BC} \Leftrightarrow \left\{ \begin{array}{l}140 = 2\left( {x - 940} \right)\\50 = 2\left( {y - 550} \right)\\2 = 2\left( {z - 9} \right)\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 1010\\y = 575\\z = 10\end{array} \right.\]
Vậy \[x\, + \,y\, + z = 1595\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.