Có hai xã cùng ở một bên bờ sông. Người ta đo được khoảng cách từ trung tâm \[A,B\] của hai xã đó đến bờ sông lần lượt là \[AA' = 118m\], \[BB' = 487m\] và \[A'B' = 492\,m\] (Hình vẽ). Các kĩ sư muốn xây một trạm cung cấp nước sạch nằm bên bờ sông cho người dân hai xã. Để tiết kiệm chi phí, các kĩ sư cần phải chọn vị trí \[M\] của trạm cung cấp nước sạch đó trên đoạn \[A'B'\] sao cho tổng khoảngcách từ hai vị trí \[A,B\] đến vị trí \[M\] là nhỏ nhất. Tính tổng khoảng cách nhỏ nhất đó (kết quả làm tròn đến hàng đơn vị).
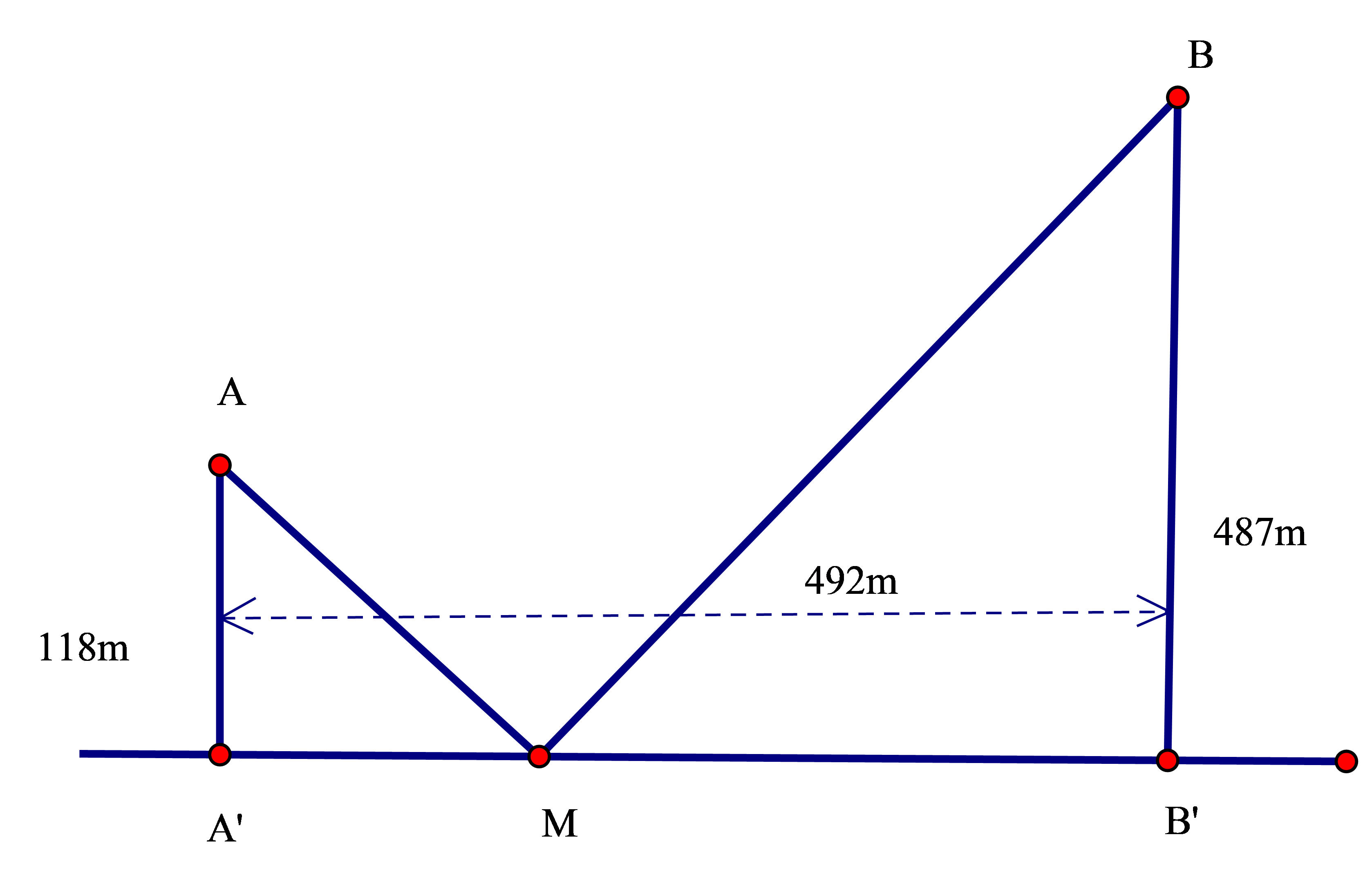
Có hai xã cùng ở một bên bờ sông. Người ta đo được khoảng cách từ trung tâm \[A,B\] của hai xã đó đến bờ sông lần lượt là \[AA' = 118m\], \[BB' = 487m\] và \[A'B' = 492\,m\] (Hình vẽ). Các kĩ sư muốn xây một trạm cung cấp nước sạch nằm bên bờ sông cho người dân hai xã. Để tiết kiệm chi phí, các kĩ sư cần phải chọn vị trí \[M\] của trạm cung cấp nước sạch đó trên đoạn \[A'B'\] sao cho tổng khoảngcách từ hai vị trí \[A,B\] đến vị trí \[M\] là nhỏ nhất. Tính tổng khoảng cách nhỏ nhất đó (kết quả làm tròn đến hàng đơn vị).

Câu hỏi trong đề: Bộ 20 đề thi Giữa kì 1 Toán 12 có đáp án !!
Quảng cáo
Trả lời:
Ta đặt \(A'M = x\), khi đó ta được:
\(MB' = 492 - x,AM = \sqrt {{x^2} + {{118}^2}} ,BM = \sqrt {{{(492 - x)}^2} + {{487}^2}} {\rm{.}}\)
Như vậy ta có hàm số \(f\left( x \right)\) được xác định bằng tổng quãng đường \(AM\) và \(MB\):
\(f\left( x \right) = \sqrt {{x^2} + {{118}^2}} + \sqrt {{{(492 - x)}^2} + {{487}^2}} {\rm{\;}}\)với\(x \in \left[ {0;492} \right]\)
Ta cần tìm giá trị nhỏ nhất của \(f\left( x \right)\) để có được quãng đường ngắn nhất và từ đó xác định được vị trí điểm \(M\).
\(f'\left( x \right) = \frac{x}{{\sqrt {{x^2} + {{118}^2}} }} - \frac{{492 - x}}{{\sqrt {{{(492 - x)}^2} + {{487}^2}} }}{\rm{.\;}}\)
\(f'\left( x \right) = 0\)\( \Leftrightarrow \frac{x}{{\sqrt {{x^2} + {{118}^2}} }} = \frac{{492 - x}}{{\sqrt {{{(492 - x)}^2} + {{487}^2}} }} \Leftrightarrow x\sqrt {{{(492 - x)}^2} + {{487}^2}} = \left( {492 - x} \right)\sqrt {{x^2} + {{118}^2}} \)
\( \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{{x^2}\left[ {{{\left( {492 - x} \right)}^2} + {{487}^2}} \right] = {{(492 - x)}^2}\left( {{x^2} + {{118}^2}} \right)}\\{0 \le x \le 492}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{{{(487x)}^2} = {{(58056 - 118x)}^2}}\\{0 \le x \le 492}\end{array}} \right.} \right.\)
\( \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{x = \frac{{58056}}{{605}}{\rm{\;hay\;}}x = - \frac{{58056}}{{369}} \Leftrightarrow x = \frac{{58056}}{{605}}}\\{0 \le x \le 492}\end{array}} \right.\)
Hàm số \(f\left( x \right)\) liên tục trên đoạn \(\left[ {0;492} \right]\). So sánh các giá trị của \(f\left( 0 \right),f\left( {\frac{{58056}}{{605}}} \right),f\left( {492} \right)\) ta có giá trị nhỏ nhất là \(f\left( {\frac{{58056}}{{605}}} \right) \approx 779,8{\rm{\;m}}\)
Khi đó quãng đường đi ngắn nhất là xấp xỉ \(779,8{\rm{\;m}}\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
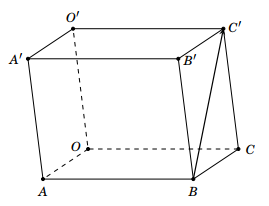
(a) Đúng: Gọi \(C'\left( {x;y;z} \right)\). Ta có \(\overrightarrow {BC'} = \left( {2; - 6;6} \right) \Rightarrow \left\{ {\begin{array}{*{20}{l}}{x - 0 = 2}\\{y - 3 = - 6}\\{z - 0 = 6}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x = 2}\\{y = - 3}\\{z = 6}\end{array}} \right.} \right.\)\( \Rightarrow C\left( {2; - 3;6} \right)\).
(b) Đúng: Gọi \(O'\left( {x;y;z} \right)\). Theo hình vẽ thì \(\overrightarrow {AO'} = \overrightarrow {BC'} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x - 1 = 2}\\{y - 1 = - 6}\\{z + 1 = 6}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x = 3}\\{y = - 5}\\{z = 5}\end{array}} \right.} \right.\)\( \Rightarrow O'\left( {3; - 5;5} \right)\)
(c) Sai: Theo hình vẽ thì \(\overrightarrow {AB'} = \overrightarrow {OC'} = \left( {2; - 3;6} \right)\).
(d) Sai: Ta có \(\overrightarrow {HK} = \overrightarrow {AB} = \left( { - 1;2;1} \right)\).
Lời giải
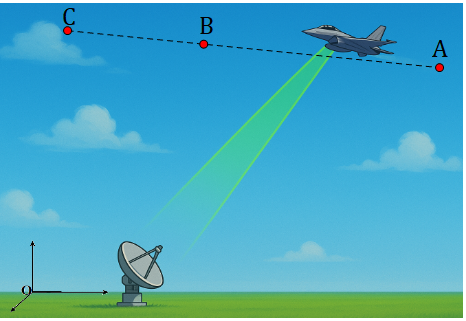
Do máy bay giữ nguyên tốc độ nên vận tốc của máy bay trên quãng đường \[AB\] và \[BC\] là như nhau. Ta có: \[\frac{{AB}}{{10}} = \frac{{BC}}{5} \Leftrightarrow AB = 2BC\].
Và máy bay giữ nguyên hướng bay nên hai vectơ \[\overrightarrow {AB} ;\,\overrightarrow {BC} \] cùng hướng.
Do đó \[\overrightarrow {AB} = 2\overrightarrow {BC} \Leftrightarrow \left\{ \begin{array}{l}140 = 2\left( {x - 940} \right)\\50 = 2\left( {y - 550} \right)\\2 = 2\left( {z - 9} \right)\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 1010\\y = 575\\z = 10\end{array} \right.\]
Vậy \[x\, + \,y\, + z = 1595\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.