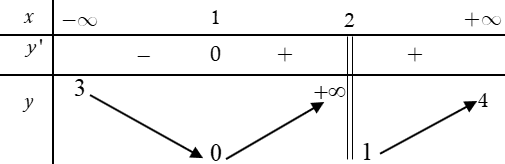
Cho hàm số \[f\left( x \right)\] xác định, liên tục trên \[\mathbb{R}\] và có bảng biến thiên sau. Khẳng định nào sau đây đúng?              

Gọi độ dài cạnh đáy của hình chóp là \(x\left( m \right)\). Do \(MN < IJ = \sqrt 2  \Rightarrow x \in \left( {0;\sqrt 2 } \right)\).

Ta có: \(OK = \frac{x}{2};OA = \frac{{AC}}{2} = \sqrt 2  \Rightarrow SK = AK = \sqrt 2  - \frac{x}{2}\).

Do vậy: \(SO = \sqrt {S{K^2} - O{K^2}}  = \sqrt {{{\left( {\sqrt 2  - \frac{x}{2}} \right)}^2} - \frac{{{x^2}}}{4}}  = \sqrt {2 - \sqrt 2 x} \).

Khi đó thể tích khối chóp là: \(V = \frac{1}{3}{x^2}\sqrt {2 - \sqrt 2 x} \).

Xét \(f\left( x \right) = \frac{1}{3}{x^2}\sqrt {2 - \sqrt 2 x} ,\,\left( {x \in \left( {0;\sqrt 2 } \right)} \right)\), ta có:

\(f'\left( x \right) = \frac{1}{3}\left( {2x\sqrt {2 - \sqrt 2 x}  - {x^2}\frac{{\sqrt 2 }}{{2\sqrt {2 - \sqrt 2 x} }}} \right) = \frac{1}{3}\left( {\frac{{4x\left( {2 - \sqrt 2 x} \right) - \sqrt 2 {x^2}}}{{2\sqrt {2 - \sqrt 2 x} }}} \right) = \frac{{8x - 5\sqrt 2 {x^2}}}{{3\left( {2\sqrt {2 - \sqrt 2 x} } \right)}}\)

\(f'\left( x \right) = 0 \Leftrightarrow 8x - 5\sqrt 2 {x^2} = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = \frac{{4\sqrt 2 }}{5}\end{array} \right.\)

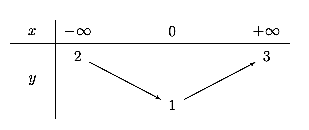
Ta có bảng biến thiên:

Sau \(t\) phút, trong bể chứa \(\left( {50t + 150} \right)\)lít nước và \(20t\)gam chất khử trùng.

Suy ra nồng độ chất khử trùng trong bể sau \(t\) phút là \(f\left( t \right) = \frac{{20t}}{{50t + 150}}\)gam/lít.

Khảo sát sự biến thiên hàm số \(f\left( t \right) = \frac{{20t}}{{50t + 150}}\), \(t \ge 0\).

Ta có: \(f'\left( t \right) = \frac{{3000}}{{{{\left( {50t + 150} \right)}^2}}} > 0,\forall t \ge 0\)

\(\mathop {\lim }\limits_{t \to  + \infty } f\left( t \right) = \mathop {\lim }\limits_{t \to  + \infty } \frac{{20t}}{{50t + 150}} = \mathop {\lim }\limits_{t \to  + \infty } \frac{{20}}{{50 + \frac{{150}}{t}}} = \frac{2}{5} = 0,4\)

Bảng biến thiên

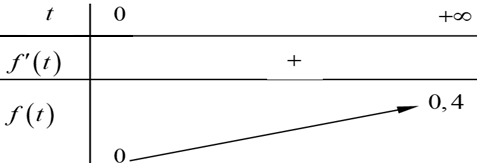
Dựa vào BBT ta thấy giá trị \(f\left( t \right)\) tăng theo \(t\) nhưng không vượt ngưỡng \(0,4\)gam/lít.

Vậy \(p = 0,4\).