Cho hàm số \(f\left( x \right)\) có đạo hàm \(f'\left( x \right) = x{\left( {x + 3} \right)^3}{\left( {x - 1} \right)^2}\). Số điểm cực trị của hàm số đã cho là
Câu hỏi trong đề: Bộ 20 đề thi Giữa kì 1 Toán 12 có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Ta có \(f'\left( x \right) = 0 \Leftrightarrow f'\left( x \right) = x{\left( {x + 3} \right)^3}{\left( {x - 1} \right)^2} = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\{\left( {x + 3} \right)^3} = 0\\{\left( {x - 1} \right)^2} = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = - 3\\x = 1\end{array} \right..\)
Bảng biến thiên:
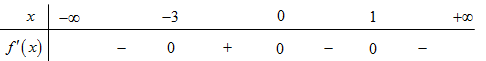
Dựa vào bảng biến thiên, ta thấy \(f'\left( x \right)\) đổi dấu từ âm sang dương khi qua nghiệm \(x = - 3\) và \(f'\left( x \right)\)đổi dấu từ dương sang âm khi qua nghiệm \(x = 0\), nên hàm số đã cho có 2 điểm cực trị.
*Phương án nhiễu A, học sinh không nhớ được các định lí về điểm cực đại và điểm cực tiểu (điểm cực trị) nên chọn bừa là hàm số có \(0\) điểm cực trị, hoặc học sinh không biết tìm ra các nghiệm của phương trình\(f'\left( x \right) = 0\) nên chọn bừa.
*Phương án nhiễu B, học sinh nhìn vào bảng xét dấu có \(1\) dấu nên suy ra hàm số có \(1\) điểm cực trị.
*Phương án nhiễu D, học sinh nhìn nhầm \(f'\left( x \right) = 0\) tại \(3\) nghiệm nên suy ra hàm số có \(3\) điểm cực trị.
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
![Cho một tấm bìa hình vuông có cạnh \[2m\]. Từ t (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/10/17-1761639676.png)
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
![Cho một tấm bìa hình vuông có cạnh \[2m\]. Từ t (ảnh 2)](https://video.vietjack.com/upload2/quiz_source1/2025/10/18-1761639705.png)
![Cho một tấm bìa hình vuông có cạnh \[2m\]. Từ t (ảnh 3)](https://video.vietjack.com/upload2/quiz_source1/2025/10/19-1761639716.png)
Gọi độ dài cạnh đáy của hình chóp là \(x\left( m \right)\). Do \(MN < IJ = \sqrt 2 \Rightarrow x \in \left( {0;\sqrt 2 } \right)\).
Ta có: \(OK = \frac{x}{2};OA = \frac{{AC}}{2} = \sqrt 2 \Rightarrow SK = AK = \sqrt 2 - \frac{x}{2}\).
Do vậy: \(SO = \sqrt {S{K^2} - O{K^2}} = \sqrt {{{\left( {\sqrt 2 - \frac{x}{2}} \right)}^2} - \frac{{{x^2}}}{4}} = \sqrt {2 - \sqrt 2 x} \).
Khi đó thể tích khối chóp là: \(V = \frac{1}{3}{x^2}\sqrt {2 - \sqrt 2 x} \).
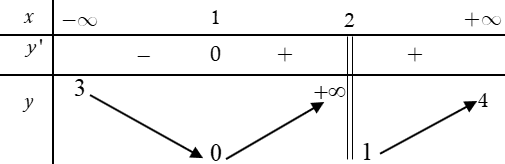
Xét \(f\left( x \right) = \frac{1}{3}{x^2}\sqrt {2 - \sqrt 2 x} ,\,\left( {x \in \left( {0;\sqrt 2 } \right)} \right)\), ta có:
\(f'\left( x \right) = \frac{1}{3}\left( {2x\sqrt {2 - \sqrt 2 x} - {x^2}\frac{{\sqrt 2 }}{{2\sqrt {2 - \sqrt 2 x} }}} \right) = \frac{1}{3}\left( {\frac{{4x\left( {2 - \sqrt 2 x} \right) - \sqrt 2 {x^2}}}{{2\sqrt {2 - \sqrt 2 x} }}} \right) = \frac{{8x - 5\sqrt 2 {x^2}}}{{3\left( {2\sqrt {2 - \sqrt 2 x} } \right)}}\)
\(f'\left( x \right) = 0 \Leftrightarrow 8x - 5\sqrt 2 {x^2} = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = \frac{{4\sqrt 2 }}{5}\end{array} \right.\)
Ta có bảng biến thiên:
![Cho một tấm bìa hình vuông có cạnh \[2m\]. Từ t (ảnh 4)](https://video.vietjack.com/upload2/quiz_source1/2025/10/20-1761639727.png)
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Sau \(t\) phút, trong bể chứa \(\left( {50t + 150} \right)\)lít nước và \(20t\)gam chất khử trùng.
Suy ra nồng độ chất khử trùng trong bể sau \(t\) phút là \(f\left( t \right) = \frac{{20t}}{{50t + 150}}\)gam/lít.
Khảo sát sự biến thiên hàm số \(f\left( t \right) = \frac{{20t}}{{50t + 150}}\), \(t \ge 0\).
Ta có: \(f'\left( t \right) = \frac{{3000}}{{{{\left( {50t + 150} \right)}^2}}} > 0,\forall t \ge 0\)
\(\mathop {\lim }\limits_{t \to + \infty } f\left( t \right) = \mathop {\lim }\limits_{t \to + \infty } \frac{{20t}}{{50t + 150}} = \mathop {\lim }\limits_{t \to + \infty } \frac{{20}}{{50 + \frac{{150}}{t}}} = \frac{2}{5} = 0,4\)
Bảng biến thiên
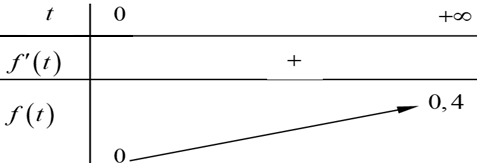
Dựa vào BBT ta thấy giá trị \(f\left( t \right)\) tăng theo \(t\) nhưng không vượt ngưỡng \(0,4\)gam/lít.
Vậy \(p = 0,4\).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
a) Tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số là 2.
b) Tập xác định của hàm số \(y = f(x)\) là \(D = \mathbb{R}\backslash {\rm{\{ }}2\} \).
c) Giá trị nhỏ nhất của hàm số bằng 0.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
a) \(f\left( x \right) = x + 2 - \frac{2}{{x + 2}},\,\forall x \in \left( { - \infty ; - 2} \right) \cup \left( { - 2; + \infty } \right)\).
b) Đồ thị hàm số có tiệm cận đứng là đường \(x = 2\).
c) Đồ thị hàm số có đường tiệm cận xiên là \(y = x + 2\).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập