PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Một cửa hàng bán quả vải thiều của Bắc Giang với giá bán là \(30000\) đồng/ 1kg. Giá nhập vào là \(16000\) đồng/1 kg. Với giá này cửa hàng ước chừng bán được 100 kg/ ngày. Cửa hàng dự định giảm giá bán, ước tính cứ giảm \(1000\) đồng/ 1kg thì số vải thiều bán được sẽ tăng thêm là 10kg.
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Một cửa hàng bán quả vải thiều của Bắc Giang với giá bán là \(30000\) đồng/ 1kg. Giá nhập vào là \(16000\) đồng/1 kg. Với giá này cửa hàng ước chừng bán được 100 kg/ ngày. Cửa hàng dự định giảm giá bán, ước tính cứ giảm \(1000\) đồng/ 1kg thì số vải thiều bán được sẽ tăng thêm là 10kg.b) Lợi nhuận tối đa theo ngày của cửa hàng là \(1600000\) đồng.
c) Nếu giá bán là \(20000\) đồng/ 1kg, khi đó cửa hàng bán được 250kg / ngày.
Câu hỏi trong đề: Bộ 20 đề thi Giữa kì 1 Toán 12 (có đáp án) !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
|
a) |
Đ |
b) |
S |
c) |
Đ |
d) |
S |
Lợi nhuận theo ngày của cửa hàng là \(\left( {30000 - 16000} \right).100 = 1400000\)Sai
Với giá \(20000\) đồng/ 1kg, khi đó cửa hàng bán được \(100 + \left( {30 - 20} \right).10 = 200\).Đúng.
Gọi \(x\) là giá tiền mà cửa hàng dự định bán \(\left( {16 \le x \le 30} \right)\).
Khi đó số kg vải bán được sẽ là \[100 + \left( {30 - x} \right).10 = 400 - 10x\]
Lợi nhuận thu được theo ngày là: \(\left( {x - 16} \right)\left( {400 - 10x} \right) = - 10{x^2} + 560x - 6400\).Sai.
\(\left( {x - 16} \right)\left( {400 - 10x} \right) = - 10{x^2} + 560x - 6400 = - 10{\left( {x - 28} \right)^2} + 1440 \le 1440\).
Vậy lợi nhuận tối đa là \(1440000\) đồng/ ngày, xảy ra khi giá bán là \(28000\) đồng/1kg.
Hot: 1000+ Đề thi cuối kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp án:
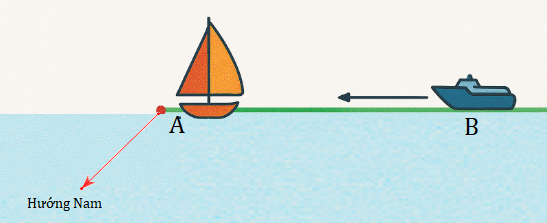
Quãng đường con tàu \(A\) đi được sau \(t\) giờ là: \(6t\) (hải lý)
Quãng đường con tàu \(B\) đi được sau \(t\) giờ là: \(8t\) (hải lý)
Sau \(t\) giờ khoảng cách giữa hai con tàu là:
\(f(t) = \sqrt {{{\left( {6t} \right)}^2} + {{\left( {10 - 8t} \right)}^2}} = \sqrt {100{t^2} - 160t + 100} = \sqrt {{{(10t - 8)}^2} + 36} \ge 6\)
Khoảng cách giữa hai con tàu ngắn nhất bằng \(6\)(hải lý) khi \(t = \frac{4}{5} = 0,8\) (giờ)
Vậy sau \(0,8\) giờ thì khoảng cách giữa hai con tàu ngắn nhất.
Lời giải
Đáp án:
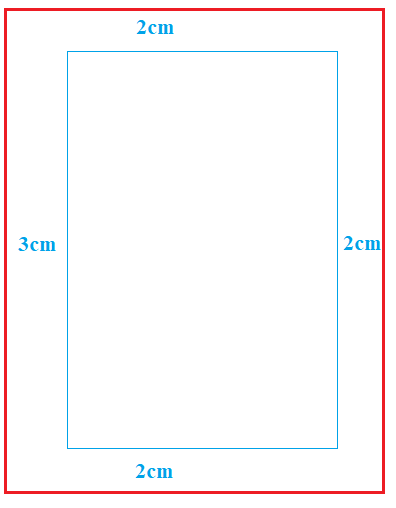
Gọi chiều dài của trang giấy là \(x\,cm\) ta có chiều rộng là \(\frac{{600}}{x}cm\).
Chiều dài và chiều rộng của phần in chữ lần lượt là \(x - 4\) và \(\frac{{600}}{x} - 5\)
Diện tích phần in chữ là \(f\left( x \right) = \left( {\frac{{600}}{x} - 5} \right)\left( {x - 4} \right) = 620 - 5x - \frac{{2400}}{x}\)
\(f'\left( x \right) = \frac{{2400}}{{{x^2}}} - 5 = 0 \Leftrightarrow x = \pm 4\sqrt {30} \)
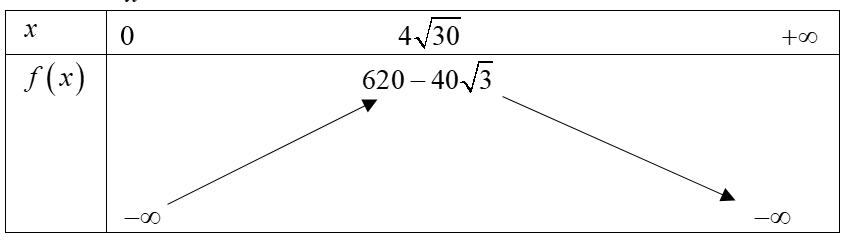
Vậy diện tích lớn nhất của phần in chữ xấp xỉ 401 \(c{m^2}\).
Câu 3
a) Tọa độ điểm \(A\left( { - 1;0;0} \right)\).
b) Tọa độ điểm \(C\left( {0;\sqrt 3 ;0} \right)\).
c) Tọa độ điểm \(A'\left( {0; - 1;\sqrt 3 } \right)\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
a) Biết hàm số có 2 điểm cực trị khi đó tổng của giá trị cực đại và giá trị cực tiểu bằng \( - 4\).
b) Đường tiệm cận xiên của đồ thị hàm số đi qua điểm \(A\left( {0;1} \right)\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập