Một vận động viên thể thao hai môn phối hợp luyện tập với một bể bơi hình chữ nhật rộng \(400\;m\), dài \(800\;m\). Vận động viên chạy phối hợp với bơi như sau: Xuất phát từ điểm \(A\), chạy đến điểm \(X\) và bơi từ điểm \(X\) đến điểm \(C\).
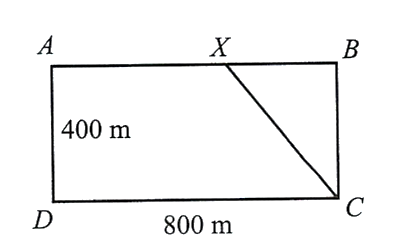
Hỏi nên chọn điểm \(X\) cách \(A\) gần bằng bao nhiêu mét để vận động viên đến \(C\) nhanh nhất ? Biết rằng vận tốc chạy là \(30\;km/h\), vận tốc bơi là \(6\;km/h\).
Một vận động viên thể thao hai môn phối hợp luyện tập với một bể bơi hình chữ nhật rộng \(400\;m\), dài \(800\;m\). Vận động viên chạy phối hợp với bơi như sau: Xuất phát từ điểm \(A\), chạy đến điểm \(X\) và bơi từ điểm \(X\) đến điểm \(C\).
Hỏi nên chọn điểm \(X\) cách \(A\) gần bằng bao nhiêu mét để vận động viên đến \(C\) nhanh nhất ? Biết rằng vận tốc chạy là \(30\;km/h\), vận tốc bơi là \(6\;km/h\).
Câu hỏi trong đề: Bộ 20 đề thi Giữa kì 1 Toán 12 (có đáp án) !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án:
Đặt \(BX = x(\;km)\), ta có: \(AX = 0,8 - x(\;km)\);
\(XC = \sqrt {{{(0,4)}^2} + {x^2}} = \sqrt {0,16 + {x^2}} (\;km)\)
Xét hàm số:
\(T(x) = \frac{{0,8 - x}}{{30}} + \frac{{\sqrt {0,16 + {x^2}} }}{6} = \frac{1}{{30}}\left( {0,8 - x + 5\sqrt {0,16 + {x^2}} } \right)(0 \le x < 0,8).\)
Ta có: \(T'(x) = \frac{1}{{30}}\left( { - 1 + \frac{{5x}}{{\sqrt {0,16 + {x^2}} }}} \right),T'(x) = 0 \Rightarrow 5x = \sqrt {0,16 + {x^2}} \).
Bình phương hai vế phương trình ta được \(0,16 + {x^2} = 25{x^2} \Leftrightarrow x = \pm \frac{{\sqrt 6 }}{{30}}\). Vì \(0 < x < 0,8\) nên \(x = \frac{{\sqrt 6 }}{{30}}\).
Bảng biến thiên của hàm số \(T(x)\) là:
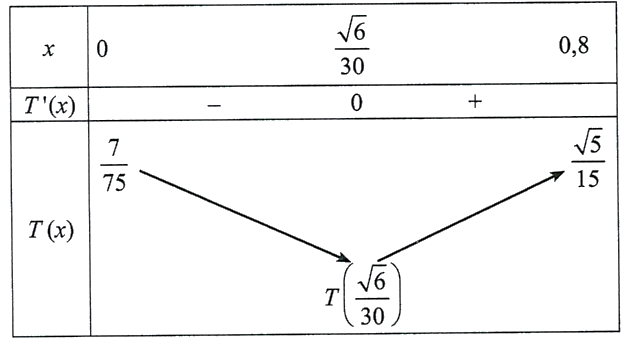
Vậy \(T(x)\) đạt giá trị nhỏ nhất bằng \(T\left( {\frac{{\sqrt 6 }}{{30}}} \right)\) khi
\(AX = 0,8 - \frac{{\sqrt 6 }}{{30}} \approx 0,718(\;km) = 718(\;m){\rm{. }}\)
Hot: 1000+ Đề thi cuối kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp án:
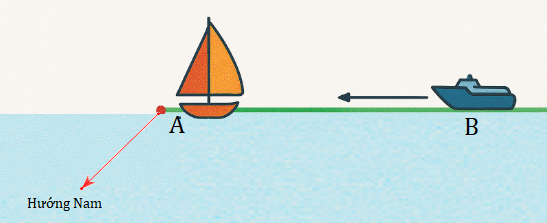
Quãng đường con tàu \(A\) đi được sau \(t\) giờ là: \(6t\) (hải lý)
Quãng đường con tàu \(B\) đi được sau \(t\) giờ là: \(8t\) (hải lý)
Sau \(t\) giờ khoảng cách giữa hai con tàu là:
\(f(t) = \sqrt {{{\left( {6t} \right)}^2} + {{\left( {10 - 8t} \right)}^2}} = \sqrt {100{t^2} - 160t + 100} = \sqrt {{{(10t - 8)}^2} + 36} \ge 6\)
Khoảng cách giữa hai con tàu ngắn nhất bằng \(6\)(hải lý) khi \(t = \frac{4}{5} = 0,8\) (giờ)
Vậy sau \(0,8\) giờ thì khoảng cách giữa hai con tàu ngắn nhất.
Lời giải
Đáp án:
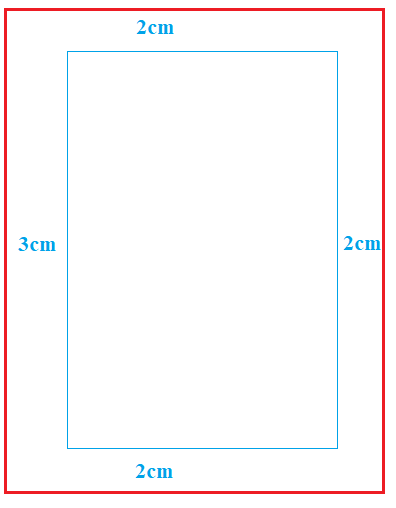
Gọi chiều dài của trang giấy là \(x\,cm\) ta có chiều rộng là \(\frac{{600}}{x}cm\).
Chiều dài và chiều rộng của phần in chữ lần lượt là \(x - 4\) và \(\frac{{600}}{x} - 5\)
Diện tích phần in chữ là \(f\left( x \right) = \left( {\frac{{600}}{x} - 5} \right)\left( {x - 4} \right) = 620 - 5x - \frac{{2400}}{x}\)
\(f'\left( x \right) = \frac{{2400}}{{{x^2}}} - 5 = 0 \Leftrightarrow x = \pm 4\sqrt {30} \)
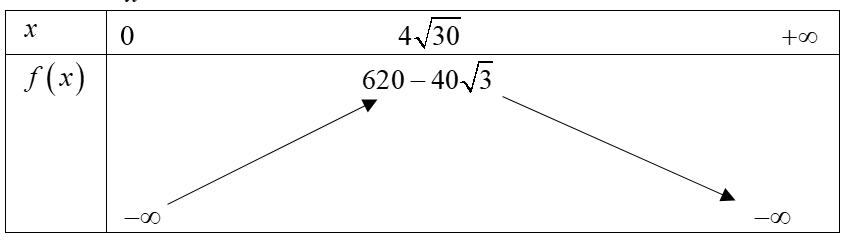
Vậy diện tích lớn nhất của phần in chữ xấp xỉ 401 \(c{m^2}\).
Câu 3
a) Tọa độ điểm \(A\left( { - 1;0;0} \right)\).
b) Tọa độ điểm \(C\left( {0;\sqrt 3 ;0} \right)\).
c) Tọa độ điểm \(A'\left( {0; - 1;\sqrt 3 } \right)\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
a) Biết hàm số có 2 điểm cực trị khi đó tổng của giá trị cực đại và giá trị cực tiểu bằng \( - 4\).
b) Đường tiệm cận xiên của đồ thị hàm số đi qua điểm \(A\left( {0;1} \right)\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
b) Lợi nhuận tối đa theo ngày của cửa hàng là \(1600000\) đồng.
c) Nếu giá bán là \(20000\) đồng/ 1kg, khi đó cửa hàng bán được 250kg / ngày.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập