PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6.
Một đường ray tàu lượn trong khu vui chơi giải trí có hình dáng được mô phỏng theo đồ thị của hàm số \(y = {x^3} - 3x + 2\), ký hiệu là (C). Để đảm bảo an toàn và tính thẩm mỹ, người ta chọn hai điểm \(A(a;b)\) và \(B(c;d)\) trên đường ray sao cho tiếp tuyến tại hai điểm này có cùng độ dốc (cùng hệ số góc). Đồng thời, đoạn đường nối hai trụ đỡ tại các điểm A và B phải vuông góc với một đường dây điện có phương trình \(x + y - 5 = 0\). Tìm \(b + d\)
PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6.
Một đường ray tàu lượn trong khu vui chơi giải trí có hình dáng được mô phỏng theo đồ thị của hàm số \(y = {x^3} - 3x + 2\), ký hiệu là (C). Để đảm bảo an toàn và tính thẩm mỹ, người ta chọn hai điểm \(A(a;b)\) và \(B(c;d)\) trên đường ray sao cho tiếp tuyến tại hai điểm này có cùng độ dốc (cùng hệ số góc). Đồng thời, đoạn đường nối hai trụ đỡ tại các điểm A và B phải vuông góc với một đường dây điện có phương trình \(x + y - 5 = 0\). Tìm \(b + d\) Câu hỏi trong đề: Bộ 20 đề thi Giữa kì 1 Toán 12 (có đáp án) !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án:
\(y = {x^3} - 3x + 2 \Rightarrow y' = 3{x^2} - 3\)
Tiếp tuyến với \(\left( C \right)\) tại \(A,B\) có cùng hệ số góc và chỉ khi \(f'\left( {{x_A}} \right) = f'\left( {{x_B}} \right) \Leftrightarrow x_A^2 = x_B^2 \Leftrightarrow \left[ \begin{array}{l}{x_A} = {x_B}\left( L \right)\\{x_A} + {x_B} = 0\end{array} \right.\)
\( \Rightarrow A,B\)đối xứng nhau qua \(I\left( {0;2} \right)\) là tâm đối xứng của \(\left( C \right).\)
\(AB \bot d:x + y - 5 = 0 \Rightarrow AB:x - y + m = 0.\)
\(AB\)qua \(I\) nên ta có \(m = 2 \Rightarrow AB:x - y + 2 = 0.\)
Khi đó hoành độ \(A,B\)thỏa mãn phương trình
\({x^3} - 3x + 2 = x + 2 \Leftrightarrow \left[ \begin{array}{l}x = 0\;(L)\\x = \pm 2\end{array} \right. \Rightarrow A\left( {2;4} \right),B\left( { - 2;0} \right)\).
Hot: 1000+ Đề thi cuối kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp án:
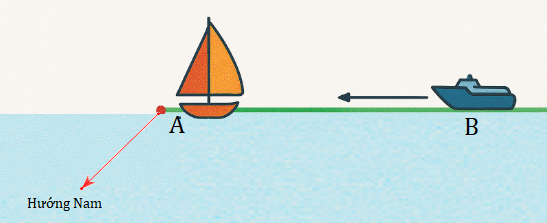
Quãng đường con tàu \(A\) đi được sau \(t\) giờ là: \(6t\) (hải lý)
Quãng đường con tàu \(B\) đi được sau \(t\) giờ là: \(8t\) (hải lý)
Sau \(t\) giờ khoảng cách giữa hai con tàu là:
\(f(t) = \sqrt {{{\left( {6t} \right)}^2} + {{\left( {10 - 8t} \right)}^2}} = \sqrt {100{t^2} - 160t + 100} = \sqrt {{{(10t - 8)}^2} + 36} \ge 6\)
Khoảng cách giữa hai con tàu ngắn nhất bằng \(6\)(hải lý) khi \(t = \frac{4}{5} = 0,8\) (giờ)
Vậy sau \(0,8\) giờ thì khoảng cách giữa hai con tàu ngắn nhất.
Lời giải
Đáp án:
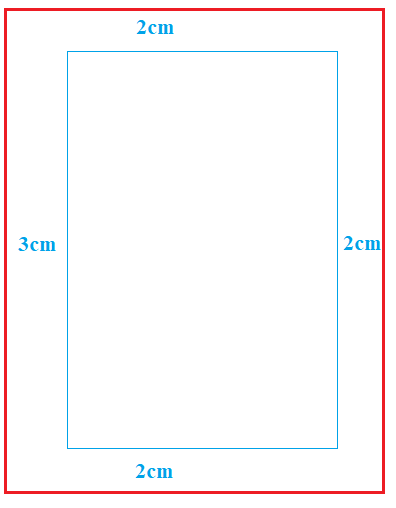
Gọi chiều dài của trang giấy là \(x\,cm\) ta có chiều rộng là \(\frac{{600}}{x}cm\).
Chiều dài và chiều rộng của phần in chữ lần lượt là \(x - 4\) và \(\frac{{600}}{x} - 5\)
Diện tích phần in chữ là \(f\left( x \right) = \left( {\frac{{600}}{x} - 5} \right)\left( {x - 4} \right) = 620 - 5x - \frac{{2400}}{x}\)
\(f'\left( x \right) = \frac{{2400}}{{{x^2}}} - 5 = 0 \Leftrightarrow x = \pm 4\sqrt {30} \)
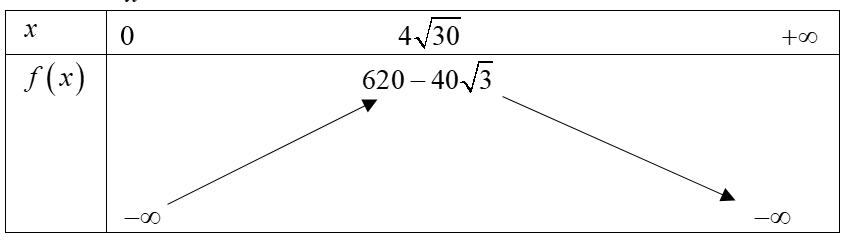
Vậy diện tích lớn nhất của phần in chữ xấp xỉ 401 \(c{m^2}\).
Câu 3
a) Tọa độ điểm \(A\left( { - 1;0;0} \right)\).
b) Tọa độ điểm \(C\left( {0;\sqrt 3 ;0} \right)\).
c) Tọa độ điểm \(A'\left( {0; - 1;\sqrt 3 } \right)\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
a) Biết hàm số có 2 điểm cực trị khi đó tổng của giá trị cực đại và giá trị cực tiểu bằng \( - 4\).
b) Đường tiệm cận xiên của đồ thị hàm số đi qua điểm \(A\left( {0;1} \right)\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
b) Lợi nhuận tối đa theo ngày của cửa hàng là \(1600000\) đồng.
c) Nếu giá bán là \(20000\) đồng/ 1kg, khi đó cửa hàng bán được 250kg / ngày.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập