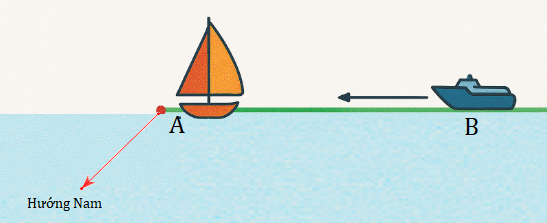
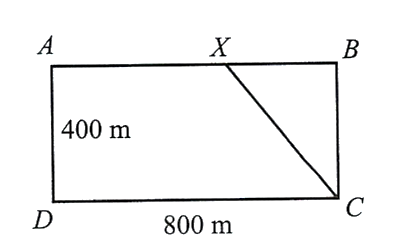
Ở trên biển, hai con tàu \(A\) và \(B\) đang ở cùng một vĩ tuyến và cách nhau \(10\) hải lý. Cả hai tàu đồng thời cùng khởi hành. Tàu \(A\) chạy về hướng Nam với vận tốc \(8\) hải lý/giờ, còn tàu \(B\) chạy về vị trí hiện tại của tàu \(A\) với vận tốc \(6\) hải lý/giờ. Hỏi sau bao nhiêu giờ thì khoảng cách giữa hai tàu là ngắn nhất (làm tròn kết quả đến hàng phần mười)?
Câu hỏi trong đề: Bộ 20 đề thi Giữa kì 1 Toán 12 (có đáp án) !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án:
Quãng đường con tàu \(A\) đi được sau \(t\) giờ là: \(6t\) (hải lý)
Quãng đường con tàu \(B\) đi được sau \(t\) giờ là: \(8t\) (hải lý)
Sau \(t\) giờ khoảng cách giữa hai con tàu là:
\(f(t) = \sqrt {{{\left( {6t} \right)}^2} + {{\left( {10 - 8t} \right)}^2}} = \sqrt {100{t^2} - 160t + 100} = \sqrt {{{(10t - 8)}^2} + 36} \ge 6\)
Khoảng cách giữa hai con tàu ngắn nhất bằng \(6\)(hải lý) khi \(t = \frac{4}{5} = 0,8\) (giờ)
Vậy sau \(0,8\) giờ thì khoảng cách giữa hai con tàu ngắn nhất.
Hot: 1000+ Đề thi cuối kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp án:
Gọi chiều dài của trang giấy là \(x\,cm\) ta có chiều rộng là \(\frac{{600}}{x}cm\).
Chiều dài và chiều rộng của phần in chữ lần lượt là \(x - 4\) và \(\frac{{600}}{x} - 5\)
Diện tích phần in chữ là \(f\left( x \right) = \left( {\frac{{600}}{x} - 5} \right)\left( {x - 4} \right) = 620 - 5x - \frac{{2400}}{x}\)
\(f'\left( x \right) = \frac{{2400}}{{{x^2}}} - 5 = 0 \Leftrightarrow x = \pm 4\sqrt {30} \)
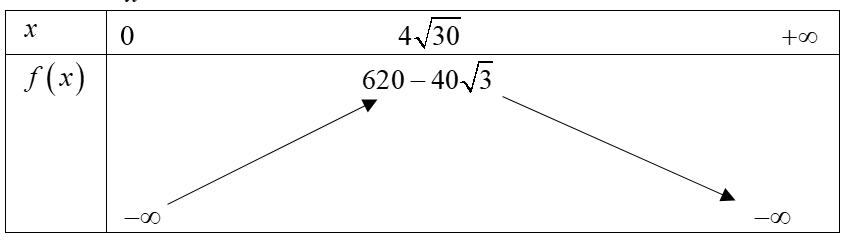
Vậy diện tích lớn nhất của phần in chữ xấp xỉ 401 \(c{m^2}\).
Câu 2
a) Tọa độ điểm \(A\left( { - 1;0;0} \right)\).
b) Tọa độ điểm \(C\left( {0;\sqrt 3 ;0} \right)\).
c) Tọa độ điểm \(A'\left( {0; - 1;\sqrt 3 } \right)\).
Lời giải
|
a) |
Đ |
b) |
Đ |
c) |
S |
d) |
Đ |
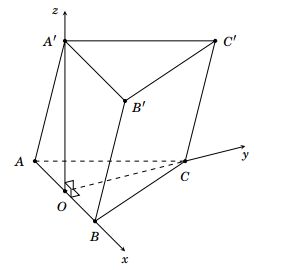
Độ dài \(OC = 2 \cdot \frac{{\sqrt 3 }}{2} = \sqrt 3 \cdot OA' = OA \cdot {\rm{tan}}{60^ \circ } = \sqrt 3 \). Với hệ trục \(Oxyz\) đã chọn như hình vẽ trên thì
a. Đúng: Điểm \(A \in Ox\), nằm ngược chiều dương và \(OA = 1\) nên \(A\left( { - 1;0;0} \right)\).
b. Đúng: Điểm \(A' \in Oy\), nằm cùng chiều dương và \(OC = \sqrt 3 \) nên \(C\left( {0;\sqrt 3 ;0} \right)\).
c. Sai: \(A' \in Oz\), nằm cùng chiều dương và \(OA' = \sqrt 3 \) nên \(A'\left( {0;0;\sqrt 3 } \right)\).
d. Đúng: Gọi \(C'\left( {x;y;z} \right)\). Ta có \(\overrightarrow {A'C'} = \overrightarrow {AC} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x - 0 = 1}\\{y - 0 = \sqrt 3 }\\{z - \sqrt 3 = 0}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x = 1}\\{y = \sqrt 3 .}\\{z = \sqrt 3 }\end{array}} \right.} \right.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
a) Biết hàm số có 2 điểm cực trị khi đó tổng của giá trị cực đại và giá trị cực tiểu bằng \( - 4\).
b) Đường tiệm cận xiên của đồ thị hàm số đi qua điểm \(A\left( {0;1} \right)\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
b) Lợi nhuận tối đa theo ngày của cửa hàng là \(1600000\) đồng.
c) Nếu giá bán là \(20000\) đồng/ 1kg, khi đó cửa hàng bán được 250kg / ngày.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập
Form KING
cái khúc
Quãng đường con tàu A đi được sau t giờ là: 6t(hải lý)
Quãng đường con tàu B đi được sau t giờ là: 8t(hải lý)
thầy cô chắc lộn tí giữa A và B chứ đúng ra phải là:
Quãng đường con tàu A đi được sau t giờ là: 8t(hải lý)
Quãng đường con tàu B đi được sau t giờ là: 6t(hải lý)
đáp đúng là 3/5 = 0,6 giờ