Câu hỏi trong đề: Bộ 10 đề thi Giữa kì 1 Toán 10 Cánh diều có đáp án !!
Quảng cáo
Trả lời:
Đáp án đúng là: D
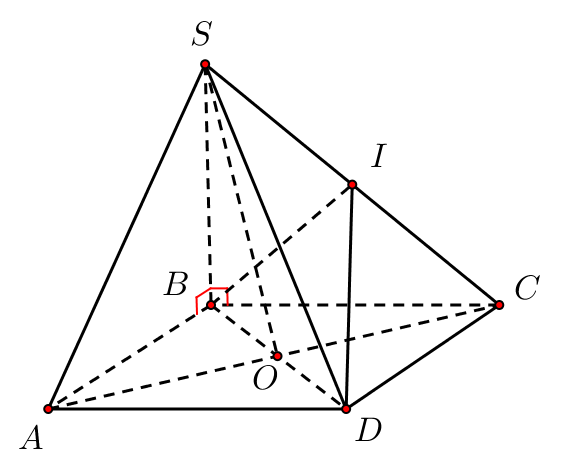
Trong tam giác \(SAC\) có \(O\) là trung điểm \(AC\), \(I\) là trung điểm \(SC\) nên \[IO\,{\rm{//}}\,SA\]
\( \Rightarrow IO\) song song với hai mặt phẳng \(\left( {SAB} \right)\) và \(\left( {SAD} \right).\)
Mặt phẳng \(\left( {IBD} \right)\) cắt \(\left( {SAC} \right)\) theo giao tuyến \(IO.\)
Mặt phẳng \(\left( {IBD} \right)\) cắt \(\left( {SBC} \right)\) theo giao tuyến \(BI\), cắt \(\left( {SCD} \right)\) theo giao tuyến \(ID\), cắt \(\left( {ABCD} \right)\) theo giao tuyến \(BD\) \( \Rightarrow \) thiết diện tạo bởi mặt phẳng \(\left( {IBD} \right)\) và hình chóp \(S.ABCD\) là tam giác \(IBD.\)
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Trọng tâm Lí, Hóa, Sinh 10 cho cả 3 bộ KNTT, CTST và CD VietJack - Sách 2025 ( 40.000₫ )
- Sách - Sổ tay kiến thức trọng tâm Vật lí 10 VietJack - Sách 2025 theo chương trình mới cho 2k9 ( 31.000₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
Lời giải
Hướng dẫn giải
Đáp án đúng là: B
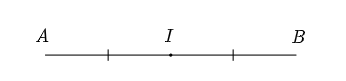
Ta có: \(A\), \(I\), \(B\) cùng thuộc đường thẳng \(AB\) nên \(\overrightarrow {AB} \) và \(\overrightarrow {AI} \) cùng phương.
Và chúng cùng hướng từ trái sang phải.
Do đó, \(\overrightarrow {AB} \) và \(\overrightarrow {AI} \) cùng hướng.
Lời giải
Gọi số bánh cỡ bé làm được là \(x\) (cái), số bánh cỡ lớn làm được là \(y\) (cái) (\(x,y \in {\mathbb{N}^*}\))
Khi đó, số điểm thưởng là: \(F\left( {x;y} \right) = 5x + 7y\).
Số kg bột mì cần dùng là: \(0,4x + 0,6y\) (kg).
Số kg bột nở cần dùng là: \(0,05x + 0,075y\) (kg).
Số kg kem béo cần dùng là: \(0,1x + 0,15y\) (kg).
Vì trong cuộc thi này chỉ được sử dụng tối đa 20 kg bột mì, 2 kg bột nở và 5 kg kem béo nên ta có hệ bất phương trình:
\(\left\{ \begin{array}{l}0,4x + 0,6y \le 20\\0,05x + 0,075y \le 2\\0,1x + 0,15y \le 5\\x \ge 0\\y \ge 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}2x + 3y \le 100\\2x + 3y \le 80\\2x + 3y \le 100\\x \ge 0\\y \ge 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}2x + 3y \le 80\\x \ge 0\\y \ge 0\end{array} \right.\) (*)
Bài toán trở thành tìm giá trị lớn nhất của hàm số \(F\left( {x;y} \right)\) trên miền nghiệm của hệ bất phương trình (*).
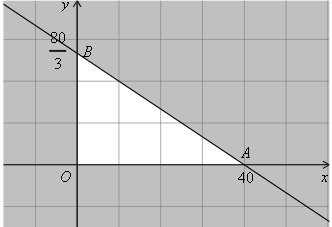
Miền nghiệm của hệ bất phương trình (*) là tam giác \(OAB\) (kể cả biên).
Hàm số \(F\left( {x;y} \right) = 5x + 7y\) sẽ đạt giá trị lớn nhất trên miền nghiệm của hệ bất phương trình (*) khi \(\left( {x;y} \right)\) là tọa độ một trong các đỉnh \(O\left( {0;0} \right)\), \(A\left( {40;0} \right)\), \(B\left( {0;\frac{{80}}{3}} \right)\).
Mà \(F\left( {0;0} \right) = 0\), \(F\left( {40;0} \right) = 200\), \(F\left( {0;\frac{{80}}{3}} \right) = \frac{{560}}{3}\).
Suy ra \(F\left( {x;y} \right)\) lớn nhất khi \(\left( {x;y} \right) = \left( {40;0} \right)\).
Do đó, cần phải làm 40 cái bánh cỡ bé để nhận được số điểm thưởng là lớn nhất.
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.