Một hồ bơi có dạng hình hộp chữ nhật có chiều cao \[3\,{\rm{m}}\] đang không chứa nước. Người ta cần thay nước mới cho hồ bơi nên dùng máy bơm để bơm nước vào hồ, giả sử \[h\left( t \right)\,\,({\rm{m)}}\] là chiều cao của mực nước đã được bơm vào tại thời điểm \[t\] giờ. Biết rằng tốc độ tăng chiều cao của mực nước tại giờ thứ \[t\] kể từ lúc bắt đầu bơm nước vào hồ là \[h'\left( t \right) = \frac{{\sqrt[3]{{t + 3}}}}{5}\]. Hỏi sau bao nhiêu giờ kể từ lúc bắt đầu bơm thì hồ đạt được độ sâu \[2,1\,{\rm{m}}\] (kết quả làm tròn đến hàng đơn vị).

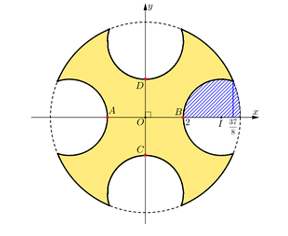
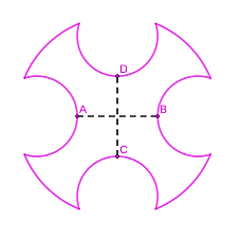
Chọn hệ trục \[Oxy\] sao cho gốc toạ độ \[O\] trùng với giao điểm \[AB,CD\].

Đường tròn lớn có phương trình: \[{x^2} + {y^2} = 25 \Rightarrow y = \pm \sqrt {25 - {x^2}} \].

Ta có \[OA = OB = OC = OD = \frac{4}{2} = 2\].

Đường tròn nhỏ có tâm trên trục \[Ox\]là \[\left( {4;0} \right)\] nên có phương trình:

\[{\left( {x - 4} \right)^2} + {y^2} = 4 \Rightarrow y = \pm \sqrt {4 - {{\left( {x - 4} \right)}^2}} \].

Ta có: \[\sqrt {25 - {x^2}} = \sqrt {4 - {{\left( {x - 4} \right)}^2}} \Leftrightarrow x = \frac{{37}}{8}\].

Gọi \(H\) là phần hình phẳng gạch chéo.

Ta có hình phẳng \(H\) giới hạn bởi các đường \[y = \sqrt {25 - {x^2}} ,y = \sqrt {4 - {{\left( {x - 4} \right)}^2}} ,y = 0\].

Đặt \({H_1} = \left\{ {y = \sqrt {4 - {{\left( {x - 4} \right)}^2}} ,y = 0,x = 2,x = \frac{{37}}{8}} \right\}\); \({H_2} = \left\{ {y = \sqrt {25 - {x^2}} ,y = 0,x = \frac{{37}}{8},x = 5} \right\}\).

Diện tích của hình \({H_1}\) là \[{S_{{H_1}}} = \int\limits_2^{\frac{{37}}{8}} {\sqrt {4 - {{\left( {x - 4} \right)}^2}} } {\rm{d}}x\].

Diện tích của hình \({H_2}\)là \({S_{{H_2}}} = \int\limits_{\frac{{37}}{8}}^5 {\sqrt {25 - {x^2}} } {\rm{d}}x\).

Khi đó diện tích của hình \(H\) là: \[{S_H} = \int\limits_2^{\frac{{37}}{8}} {\sqrt {4 - {{\left( {x - 4} \right)}^2}} } {\rm{d}}x + \int\limits_{\frac{{37}}{8}}^5 {\sqrt {25 - {x^2}} } {\rm{d}}x\].

Diện tích của đường tròn lớn là: \({S_1} = \pi \cdot {5^2} = 25\pi \).

Diện tích phần sơn 1 mặt của chi tiết máy

\[S = 25\pi - 8{S_H} = 25\pi - 8\left( {\int\limits_2^{\frac{{37}}{8}} {\sqrt {4 - {{\left( {x - 4} \right)}^2}} } {\rm{d}}x + \int\limits_{\frac{{37}}{8}}^5 {\sqrt {25 - {x^2}} } {\rm{d}}x} \right) \approx 39,7\,({\rm{d}}{{\rm{m}}^{\rm{2}}}) = 0,397({{\rm{m}}^{\rm{2}}})\].

Chi phí để sơn hoàn thiện chi tiết máy: \[2 \cdot 0,397 \cdot 82 \approx 65\] (nghìn đồng).

Đáp án: 65.

a) Sai. Ta có \[h\left( t \right) = \int {v\left( t \right){\rm{dt}} = - 0,04{t^3} + 0,6{t^2} + C} \].

Tại thời điểm xuất phát \(\left( {t = 0} \right)\), độ cao của khinh khí cầu là 520 m nên

\[h\left( 0 \right) = 520 \Rightarrow C = 520\].

Vậy \[h\left( t \right) = - 0,04{t^3} + 0,6{t^2} + 520\].

b) Đúng. Tại thời điểm \(t = 3\) phút, độ cao của khinh khí cầu là \(h\left( 3 \right) = 524,32\) m.

c) Đúng. Ta có \(h'\left( t \right) = v\left( t \right) = - 0,12{t^2} + 1,2t\), suy ra \(h'\left( t \right) = 0 \Leftrightarrow \left[ \begin{array}{l}t = 0\\t = 10\end{array} \right.\).

Ta có bảng biến thiên:

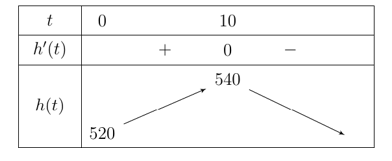
Vậy độ cao tối đa của khinh khí cầu là 540 m.

d) Đúng. Khi trở lại độ cao như lúc xuất phát thì

\(h\left( t \right) = 520 \Leftrightarrow - 0,04{t^3} + 0,6{t^2} + 520 = 520 \Leftrightarrow \left[ \begin{array}{l}t = 0\\t = 15\end{array} \right.\).

Vậy sau 15 phút thì khinh khí cầu quay trở lại độ cao như lúc đầu.