Khuôn viên nhà bạn Thùy Dương có dạng nửa hình tròn, trên đó người thiết kế phần để trồng hoa có dạng của một cánh hoa hình parabol có đỉnh trùng với tâm và có trục đối xứng vuông góc với đường kính của nửa hình tròn, hai đầu mút của cánh hoa nằm trên nửa đường tròn và cách nhau một khoảng bằng 4 m. Phần còn lại của khuôn viên dành để trồng cỏ nhung Nhật. Biết các kích thước cho như hình vẽ, chi phí trồng hoa và cỏ nhung Nhật tương ứng là 250 000 đồng/m2 và 150 000 đồng/m2. Hỏi chi phí để trồng hoa và trồng cỏ nhung Nhật trong khuôn viên đó hết bao nhiêu triệu đồng (làm tròn kết quả đến hàng phần chục)?
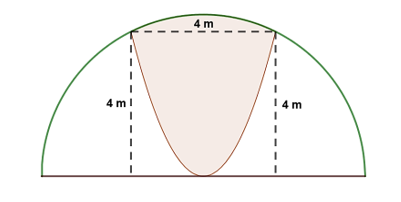
Khuôn viên nhà bạn Thùy Dương có dạng nửa hình tròn, trên đó người thiết kế phần để trồng hoa có dạng của một cánh hoa hình parabol có đỉnh trùng với tâm và có trục đối xứng vuông góc với đường kính của nửa hình tròn, hai đầu mút của cánh hoa nằm trên nửa đường tròn và cách nhau một khoảng bằng 4 m. Phần còn lại của khuôn viên dành để trồng cỏ nhung Nhật. Biết các kích thước cho như hình vẽ, chi phí trồng hoa và cỏ nhung Nhật tương ứng là 250 000 đồng/m2 và 150 000 đồng/m2. Hỏi chi phí để trồng hoa và trồng cỏ nhung Nhật trong khuôn viên đó hết bao nhiêu triệu đồng (làm tròn kết quả đến hàng phần chục)?

Quảng cáo
Trả lời:
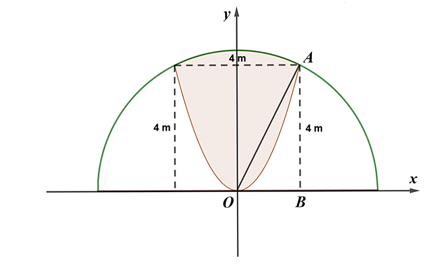
Chọn hệ trục tọa độ \(Oxy\) như hình vẽ.
Xét parabol có đỉnh là gốc tọa độ và đi qua điểm \(\left( {2;4} \right)\): Phương trình \(\left( P \right)\) có dạng \(y = a{x^2}\).
Vì \(A\left( {2;4} \right) \in \left( P \right)\) nên \(4 = a \cdot {2^2} \Leftrightarrow a = 1 \Rightarrow \left( P \right):y = {x^2}\).
Xét \(\Delta OAB\) vuông tại \(B\), theo định lý Pythagore ta có:
\(O{A^2} = A{B^2} + O{B^2} = {4^2} + {2^2} = 16 + 4 = 20 \Rightarrow R = OA = 2\sqrt 5 \).
Phương trình đường tròn \(\left( C \right)\) có tâm \(O\), bán kính \(R = 2\sqrt 5 \) là:
\({x^2} + {y^2} = 20\)\( \Rightarrow \left| y \right| = \sqrt {20 - {x^2}} \).
Diện tích phần trồng hoa là: \({S_1} = \int\limits_{ - 2}^2 {\left( {\sqrt {20 - {x^2}} - {x^2}} \right)} \,{\rm{d}}x\).
Diện tích trồng cỏ nhung Nhật là: \({S_2} = \frac{{\pi {R^2}}}{2} - {S_1} = 10\pi - {S_1}\).
Tổng chi phí để trồng hoa và trồng cỏ nhung Nhật trong khuôn viên đó là:
\(250\,000{S_1} + 150\,000{S_2} = 250\,000{S_1} + 150\,000\left( {10\pi - {S_1}} \right) \approx 5\,906\,351\) (đồng) \( \approx 5,9\) (triệu đồng).
Vậy chi phí để trồng hoa và trồng cỏ nhung Nhật trong khuôn viên nhà bạn Thùy Dương gần bằng 5,9 triệu đồng.
Đáp án: 5,9.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- 250+ Công thức giải nhanh môn Toán 12 (chương trình mới) ( 18.000₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
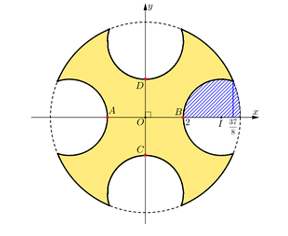
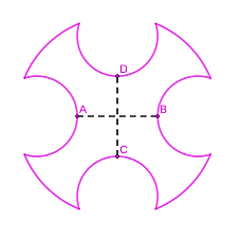
Chọn hệ trục \[Oxy\] sao cho gốc toạ độ \[O\] trùng với giao điểm \[AB,CD\].
Đường tròn lớn có phương trình: \[{x^2} + {y^2} = 25 \Rightarrow y = \pm \sqrt {25 - {x^2}} \].
Ta có \[OA = OB = OC = OD = \frac{4}{2} = 2\].
Đường tròn nhỏ có tâm trên trục \[Ox\]là \[\left( {4;0} \right)\] nên có phương trình:
\[{\left( {x - 4} \right)^2} + {y^2} = 4 \Rightarrow y = \pm \sqrt {4 - {{\left( {x - 4} \right)}^2}} \].
Ta có: \[\sqrt {25 - {x^2}} = \sqrt {4 - {{\left( {x - 4} \right)}^2}} \Leftrightarrow x = \frac{{37}}{8}\].
Gọi \(H\) là phần hình phẳng gạch chéo.
Ta có hình phẳng \(H\) giới hạn bởi các đường \[y = \sqrt {25 - {x^2}} ,y = \sqrt {4 - {{\left( {x - 4} \right)}^2}} ,y = 0\].
Đặt \({H_1} = \left\{ {y = \sqrt {4 - {{\left( {x - 4} \right)}^2}} ,y = 0,x = 2,x = \frac{{37}}{8}} \right\}\); \({H_2} = \left\{ {y = \sqrt {25 - {x^2}} ,y = 0,x = \frac{{37}}{8},x = 5} \right\}\).
Diện tích của hình \({H_1}\) là \[{S_{{H_1}}} = \int\limits_2^{\frac{{37}}{8}} {\sqrt {4 - {{\left( {x - 4} \right)}^2}} } {\rm{d}}x\].
Diện tích của hình \({H_2}\)là \({S_{{H_2}}} = \int\limits_{\frac{{37}}{8}}^5 {\sqrt {25 - {x^2}} } {\rm{d}}x\).
Khi đó diện tích của hình \(H\) là: \[{S_H} = \int\limits_2^{\frac{{37}}{8}} {\sqrt {4 - {{\left( {x - 4} \right)}^2}} } {\rm{d}}x + \int\limits_{\frac{{37}}{8}}^5 {\sqrt {25 - {x^2}} } {\rm{d}}x\].
Diện tích của đường tròn lớn là: \({S_1} = \pi \cdot {5^2} = 25\pi \).
Diện tích phần sơn 1 mặt của chi tiết máy
\[S = 25\pi - 8{S_H} = 25\pi - 8\left( {\int\limits_2^{\frac{{37}}{8}} {\sqrt {4 - {{\left( {x - 4} \right)}^2}} } {\rm{d}}x + \int\limits_{\frac{{37}}{8}}^5 {\sqrt {25 - {x^2}} } {\rm{d}}x} \right) \approx 39,7\,({\rm{d}}{{\rm{m}}^{\rm{2}}}) = 0,397({{\rm{m}}^{\rm{2}}})\].
Chi phí để sơn hoàn thiện chi tiết máy: \[2 \cdot 0,397 \cdot 82 \approx 65\] (nghìn đồng).
Đáp án: 65.
Lời giải
Ta có \[h\left( t \right) = \int {h'\left( t \right){\rm{d}}t} = \frac{1}{5}\int {{{\left( {t + 3} \right)}^{\frac{1}{3}}}{\rm{d}}t} = \frac{3}{{20}}{\left( {t + 3} \right)^{\frac{4}{3}}} + C\].
\[h\left( 0 \right) = 0 \Leftrightarrow \frac{{9\sqrt[3]{3}}}{{20}} + C = 0 \Leftrightarrow C = - \frac{{9\sqrt[3]{3}}}{{20}} \to h\left( t \right) = \frac{3}{{20}}{\left( {t + 3} \right)^{\frac{4}{3}}} - \frac{{9\sqrt[3]{3}}}{{20}}\].
\[h\left( t \right) = 2,1 \Leftrightarrow \frac{3}{{20}}{\left( {t + 3} \right)^{\frac{4}{3}}} - \frac{{9\sqrt[3]{3}}}{{20}} = 2,1 \Leftrightarrow {\left( {t + 3} \right)^{\frac{4}{3}}} \approx 18,33 \Rightarrow t \approx 6\].
Vậy sau khi bơm khoảng 6 giờ thì độ sâu của mực nước trong hồ là 2,1 m.
Đáp án: 6.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.