Một đèn thả gỗ có dạng hình chóp cụt đều như hình bên. Đáy và mặt trên là các hình vuông tương ứng có cạnh bằng \(40{\rm{cm, 20cm}}\), cạnh bên của đèn dài \(10\sqrt 5 \,{\rm{cm}}\). Mặt bên và mặt trên của đèn tạo thành góc nhị diện có số đo bằng bao nhiêu độ?

Câu hỏi trong đề: Đề ôn luyện Toán Chương 5. Hình học không gian (đề số 1) !!
Quảng cáo
Trả lời:
Mô hình hóa chiếc đèn như hình dưới đây.
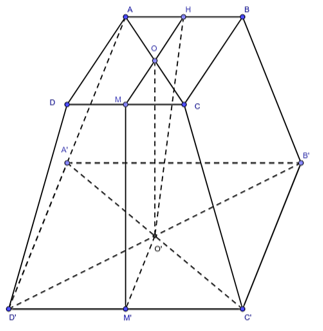
Gọi \(M,{\rm{ }}M'\) lần lượt là trung điểm của cạnh \(DC\) và \(D'C'\). Dễ chứng minh \(MM' \bot DC\) và \(OM \bot DC\) (\(OM\) là đường trung bình của \(\Delta ACD\)).
Ta có \[\left\{ \begin{array}{l}\left( {ABCD} \right) \cap \left( {DCC'D'} \right) = DC\\OM \subset \left( {ABCD} \right),OM \bot DC\\MM' \subset \left( {DCC'D'} \right),MM' \bot DC\end{array} \right.\] nên \(\widehat {OMM'}\) là góc phẳng nhị diện của góc nhị diện tạo bởi mặt bên và mặt trên của đèn.
Trong mặt phẳng \(\left( {ABCD} \right)\), gọi \(H = OM \cap AB\), khi đó \(H\) là trung điểm của \(AB\).
Ta có \(\left\{ \begin{array}{l}HM\,{\rm{//}}\,AD,\,\,HM = AD = 20\,\,{\rm{cm}}\\O'M'\,{\rm{//}}\,A'D',\,\,O'M' = \frac{1}{2}A'D' = \frac{{40}}{2} = 20\,\,{\rm{cm}}\\AD\,{\rm{//}}\,A'D'\end{array} \right.\)\( \Rightarrow \left\{ \begin{array}{l}HM\,{\rm{//}}\,O'M'\\HM = O'M'\end{array} \right.\)\( \Rightarrow HMM'O'\) là hình bình hành.
Dễ chứng minh \(BDO'B'\) là hình bình hành, suy ra \(O'D = BB' = 10\sqrt 5 \,\,{\rm{cm}}\).
\(OD = \frac{1}{2}BD = \frac{1}{2} \cdot 20\sqrt 2 = 10\sqrt 2 \,{\rm{cm}}\).
\(OO' = \sqrt {O'{D^2} - O{D^2}} = \sqrt {{{\left( {10\sqrt 5 } \right)}^2} - {{\left( {10\sqrt 2 } \right)}^2}} = 10\sqrt 3 \,\,{\rm{cm}}\).
\(OH = \frac{1}{2}BC = 10\,{\rm{cm}}\) (\(OH\) là đường trung bình của \(\Delta ABC\)).
Xét \(\Delta OO'H\) vuông tại \(O\), \(\tan \widehat {OHO'} = \frac{{OO'}}{{OH}} = \frac{{10\sqrt 3 }}{{10}} = \sqrt 3 \Rightarrow \widehat {OHO'} = 60^\circ \).
Mà \(HMM'O'\) là hình bình hành nên \(\widehat {OMM'} + \widehat {OHO'} = 180^\circ \Rightarrow \widehat {OMM'} = 120^\circ \).
Đáp án: 120.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
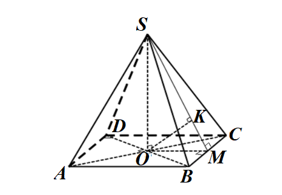
\(\left. \begin{array}{l}BC \bot OM\\BC \bot SO\left( {SO \bot \left( {ABCD} \right)} \right)\end{array} \right\} \Rightarrow BC \bot \left( {SOM} \right)\). Mà \(OK \subset \left( {SOM} \right) \Rightarrow BC \bot OK\).
Lại có \(SM \bot OK \Rightarrow OK \bot \left( {SBC} \right)\). Do đó \(d\left( {O,\left( {SBC} \right)} \right) = OK\). Chọn A.
Lời giải
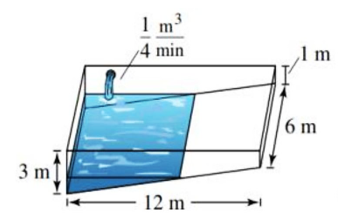
Xét các điểm như hình vẽ.
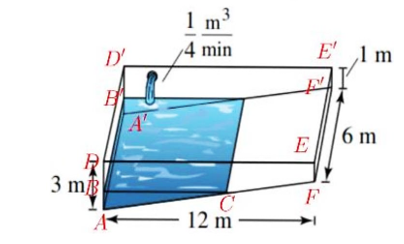
Ta có \(\frac{{BC}}{{DE}} = \frac{{AB}}{{AD}} \Rightarrow BC = \frac{{AB \cdot DE}}{{AD}} = \frac{{1 \cdot 12}}{3} = 4{\rm{\;}}\left( {\rm{m}} \right)\).
Khi mặt hồ phẳng lặng, phần nước đã có trong hồ bơi có dạng hình lăng trụ đứng tam giác.
\({S_{ABC}} = \frac{1}{2}AB \cdot BC = \frac{1}{2} \cdot 1 \cdot 4 = 2\,\,\left( {{{\rm{m}}^{\rm{2}}}} \right)\).
Thể tích nước đang có trong hồ bơi là \({V_1} = {S_{ABC}} \cdot AA' = 2 \cdot 6 = 12\left( {{{\rm{m}}^3}} \right)\).
Lại có \({S_{ADEF}} = \frac{{\left( {AD + EF} \right) \cdot DE}}{2} = \frac{{\left( {3 + 1} \right) \cdot 12}}{2} = 24\left( {{{\rm{m}}^2}} \right)\).
Thể tích hồ bơi là \(V = {S_{ADEF}}_{\rm{\;}} \cdot AA' = 24 \cdot 6 = 144\,\left( {{{\rm{m}}^3}} \right)\).
Thể tích nước cần bơm vào là \(0,75V - {V_1} = 0,75 \cdot 144 - 12 = 96\,\,\left( {{{\rm{m}}^3}} \right)\).
Thời gian bơm là \(96:0,25 = 384\) (phút).
Đáp án: 384.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.