Cho hai đường thẳng \(\left( d \right):y = 2x + 1\) và \(\left( {d'} \right):y = 2x + 2.\) Khi đó:
A. \(\left( d \right)\) cắt \(\left( {d'} \right).\)
B. \(\left( d \right)\;{\rm{//}}\;\left( {d'} \right).\)
C. \(\left( d \right)\) trùng \(\left( {d'} \right).\)
D. \(\left( d \right)\) vuông góc \(\left( {d'} \right).\)
Quảng cáo
Trả lời:
Đáp án đúng là: B
Vì \(2 = 2;\;\,1 \ne 2\) nên \(\left( d \right)\;{\rm{//}}\;\left( {d'} \right).\)
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
a) Hệ số góc của đường thẳng \(\left( d \right)\) là số dương
Lời giải
a) Sai.
Vì đường thẳng \(\left( d \right)\) đi qua điểm \(A\left( {1;\;2} \right)\) nên \(2 = a \cdot 1 + 3\) suy ra \(a = - 1.\)
Vậy hệ số góc của đường thẳng \(\left( d \right)\) là số âm.
b) Sai.
Với \(a = - 1\) thì \(\left( d \right):\;\,y = - x + 3.\)
Vì \(B\) là giao điểm của đường thẳng \(\left( d \right)\) và trục \(Ox\) nên tung độ của điểm \(B\) bằng 0.
Do đó, \(0 = - x + 3,\) suy ra \(x = 3.\) Do đó, \(B\left( {3;\;\,0} \right).\)
Vì \(C\) là giao điểm của đường thẳng \(\left( d \right)\) và trục \(Oy\) nên hoành độ của điểm \(C\) bằng 0.
Do đó, \(y = - 0 + 3.\) Do đó, \(C\left( {0;\;\,3} \right).\)
c) Đúng.
Đường thẳng \(\left( d \right)\) được vẽ như hình vẽ dưới đây:
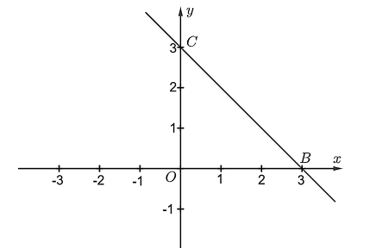
Vì \(OB = OC = 3\) và tam giác \(BOC\) vuông tại \(O\) nên tam giác \(BOC\) là tam giác vuông cân tại \(O.\)
d) Sai.
Vì tam giác \(BOC\) vuông cân tại \(O\) nên \(\widehat {OBC} = 45^\circ .\)
Do đó, góc tạo bởi đồ thị hàm số đã cho và trục hoành là: \(180^\circ - 45^\circ = 135^\circ .\)
Vậy góc tạo bởi đồ thị hàm số đã cho và trục hoành bằng \(135^\circ .\)
Câu 2
Lời giải
Đáp án đúng là: A
Các đường thẳng \(y = x - 2;\;\,y = 1 - x;\;\,y = 2x + 1;\;\,y = - x - 1\) có hệ số góc lần lượt là \(1;\;\, - 1;\;\,2;\;\, - 1.\)
Do đó, chọn đáp án A.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.