Chọn khẳng định đúng.

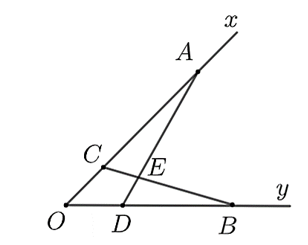
a) Sai.

Vì \(OA \cdot OC = OB \cdot OD\) nên \(\frac{{OA}}{{OB}} = \frac{{OD}}{{OC}}.\)

b) Đúng.

\(\Delta AOD\) và \(\Delta BOC\) có: \(\frac{{OA}}{{OB}} = \frac{{OD}}{{OC}},\;\,\widehat O\) chung nên \(\Delta AOD \sim \Delta BOC\;\,\left( {{\rm{c}}{\rm{.g}}{\rm{.c}}} \right).\)

c) Sai.

Vì \(\Delta AOD \sim \Delta BOC\) nên \(\widehat {EAC} = \widehat {EBD}.\)

\(\Delta ACE\) và \(\Delta BDE\) có: \(\widehat {EAC} = \widehat {EBD},\;\,\widehat {AEC} = \widehat {BED}\) (hai góc đối đỉnh).

Do đó, \(\Delta ACE \sim \Delta BDE\;\,\left( {{\rm{g}}{\rm{.g}}} \right).\)

d) Đúng.

Vì \(\Delta ACE \sim \Delta BDE\) nên \(\frac{{AE}}{{BE}} = \frac{{CE}}{{DE}}\) suy ra \(AE \cdot ED = CE \cdot EB.\)

a) Đúng.

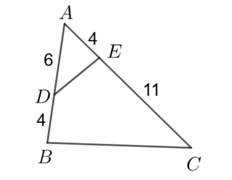
\(\Delta AMN\) và \(\Delta ACB\) có: \(\widehat {ANM} = \widehat {ABC},\;\,\widehat A\) chung nên \(\Delta AMN \sim \Delta ACB\;\,\left( {{\rm{g}}{\rm{.g}}} \right).\)

b) Sai.

Vì \(\Delta AMN \sim \Delta ACB\) nên \(\frac{{AN}}{{AB}} = \frac{{AM}}{{AC}}.\) Suy ra \(\frac{{AN}}{{AM}} = \frac{{AB}}{{AC}}.\)

c) Đúng.

\(\Delta ANB\) và \(\Delta AMC\) có: \(\frac{{AN}}{{AM}} = \frac{{AB}}{{AC}};\;\,\widehat A\) chung nên \(\Delta ANB \sim \Delta AMC\;\,\left( {{\rm{c}}{\rm{.g}}{\rm{.c}}} \right).\) Suy ra \(\widehat {OBM} = \widehat {OCN}.\)

d) Sai.

\(\Delta MOB\) và \(\Delta CON\) có: \(\widehat {OBM} = \widehat {OCN};\;\,\widehat {MOB} = \widehat {NOC}\) (hai góc đối đỉnh).

Suy ra \(\Delta MOB \sim \Delta NOC\;\,\left( {{\rm{g}}{\rm{.g}}} \right).\)