Cho tam giác \(ABC\). Trên cạnh \(AB,AC\) lần lượt lấy các điểm \(E,D\) sao cho \(AC = 3AE\) và \(AD = \frac{1}{3}AB\). Gọi \(I\) là giao điểm của \(BD\) và \(EC\). Biết rằng .
Quảng cáo
Trả lời:
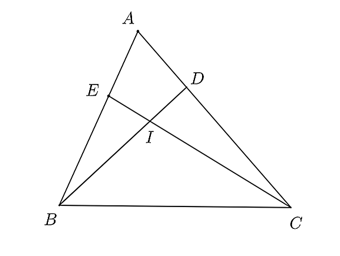
a) Đúng.
Theo đề, ta có nên \(\widehat {ADB} = \widehat {AEC}\) (hai góc tương ứng).
Do đó ý a) đúng.
b) Đúng.
Ta có: \(AC = 3AE\) hay \(\frac{{AE}}{{AC}} = \frac{1}{3}\); \(AD = \frac{1}{3}AB\) hay \(\frac{{AD}}{{AB}} = \frac{1}{3}\).
Suy ra \(\frac{{AE}}{{AC}} = \frac{{AD}}{{AB}} = \frac{1}{3}\). Do đó, ý b) đúng.
c) Sai.
Xét \(\Delta ADE\) và \(\Delta ABC\), có:
\(\frac{{AE}}{{AC}} = \frac{{AD}}{{AB}} = \frac{1}{3}\) (cmt)
\(\widehat A\) chung (gt)
Do đó, \(\Delta ADE \sim \Delta ABC\) (c.g.c)
Do đó, ý c) sai.
d) Đúng.
Vì \(\Delta ABD \sim \Delta ACE\) nên \(\widehat {ABD} = \widehat {ACE}\) (2 góc tương ứng) (1)
Lại có, \(\widehat {EIB} = \widehat {DIC}\) (hai góc đối đỉnh) (2)
Từ (1) và (2) suy ra (g.g)
Suy ra \(\frac{{IE}}{{ID}} = \frac{{IB}}{{IC}}\) suy ra \(IE.IC = IB.ID\).
Do đó, ý d) đúng.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
Lời giải
Đáp án đúng là: C
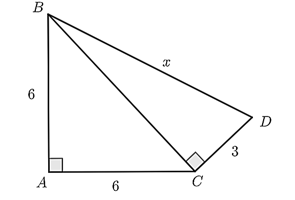
Xét \(\Delta ABC\) vuông tại \(B,\) theo định lí Pythagore ta có:
\(A{C^2} = A{B^2} + B{C^2}\) nên \(B{C^2} = A{C^2} - A{B^2} = {13^2} - {5^2} = 144.\)
Do đó \(BC = 12{\rm{\;cm}}.\)
Câu 2
Lời giải
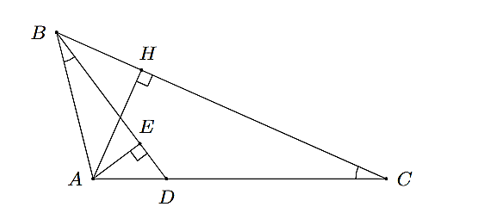
a) Đúng.
Xét \(\Delta ABD\) và \(\Delta ACB\) có: \(\widehat {ABD} = \widehat {ACB}\) (gt) và \(\widehat {BAD} = \widehat {CAB}\) (góc chung)
Suy ra \(\Delta ABD \sim \Delta ACB\) (g.g)
b) Đúng.
Do \(\Delta ABD \sim \Delta ACB\) (g.g) nên \(\widehat {ADB} = \widehat {ABC}\) (hai góc tương ứng)
c) Sai.
Do \(\Delta ABD \sim \Delta ACB\) nên \(\frac{{AB}}{{AC}} = \frac{{AD}}{{AB}}\) hay \(AD = \frac{{A{B^2}}}{{AC}} = \frac{{{2^2}}}{4} = 1{\rm{ cm}}\).
Lại có: \(DC + AD = AC\) nên \(DC = AC - AD = 4 - 1 = 3{\rm{ cm}}\).
d) Đúng.
Ta có: \(\widehat {ADB} = \widehat {DBC} + \widehat {DCB}\) (tính chất góc ngoài tam giác)
\(\widehat {ABH} = \widehat {ABD} + \widehat {DBC}\).
Mà từ giả thiết có \(\widehat {ABD} = \widehat {ACB}\) nên \(\widehat {ADB} = \widehat {ABH}\).
Xét \(\Delta EDA\) và \(\Delta HBA\), có: \(\widehat {AED} = \widehat {AHB} = 90^\circ \) (gt) và \(\widehat {ADE} = \widehat {ABH}\) (cmt)
Suy ra \(\Delta HBA \sim \Delta EDA\) (g.g)
Suy ra \(\frac{{AB}}{{AD}} = \frac{{AH}}{{EA}} = \frac{{BH}}{{AC}} = \frac{2}{1} = 2\).
Do đó, \(\frac{{{S_{ABH}}}}{{{S_{ADE}}}} = \frac{{AH}}{{EA}}.\frac{{BH}}{{AC}} = 2.2 = 4\) hay \({S_{ABH}} = 4{S_{ADE}}\).
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.