Cho góc \[\alpha \] thỏa mãn \(\frac{\pi }{2} < \alpha < \pi \) và \(\sin \alpha = \frac{4}{5}.\) Giá trị của \(M = \sin 2\left( {\alpha + \pi } \right)\) là
A. \(M = - \frac{{24}}{{25}}.\)
B. \(M = \frac{{24}}{{25}}.\)
C. \(M = - \frac{{12}}{{25}}.\)
D. \(M = \frac{{12}}{{25}}.\)
Câu hỏi trong đề: Bộ 10 đề thi cuối kì 1 Toán 11 Cánh diều có đáp án !!
Quảng cáo
Trả lời:
Đáp án đúng là: A
Ta có: \(M = \sin 2\left( {\alpha + \pi } \right) = \sin \left( {2\alpha + 2\pi } \right) = \sin 2\alpha = 2\sin \alpha .\cos \alpha .\)
Từ hệ thức \({\sin ^2}\alpha + {\cos ^2}\alpha = 1 \Rightarrow \cos \alpha = \pm \sqrt {1 - {{\sin }^2}\alpha } = \pm \sqrt {1 - {{\left( {\frac{4}{5}} \right)}^2}} = \pm \frac{3}{5}.\)
Do \(\frac{\pi }{2} < \alpha < \pi \Rightarrow \cos \alpha < 0 \Rightarrow \cos \alpha = - \frac{3}{5}.\)
Thay \(\sin \alpha = \frac{4}{5}\) và \(\cos \alpha = - \frac{3}{5}\) vào \(M,\) ta được \(M = 2.\frac{4}{5}.\left( { - \frac{3}{5}} \right) = - \frac{{24}}{{25}}.\)
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Trọng tâm Sử, Địa, GD KTPL 11 cho cả 3 bộ Kết nối, Chân trời, Cánh diều VietJack - Sách 2025 ( 38.000₫ )
- Sách - Sổ tay kiến thức trọng tâm Vật lí 11 VietJack - Sách 2025 theo chương trình mới cho 2k8 ( 45.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải

a) Vì \(ABCD\) là hình bình hành tâm \(O\) nên \(O\) là trung điểm của \(AC,\,\,BD.\)
Xét \(\Delta SBD\) có: \(O,\,\,M\) lần lượt là trung điểm của \(BD,\,\,SB.\)
Suy ra \(OM\) là đường trung bình của \(\Delta SBD.\)
\( \Rightarrow OM//SD.\)
Hơn nữa \(SD \subset \left( {SCD} \right);\,\,OM\,\, \not\subset \left( {SCD} \right).\)
\( \Rightarrow OM{\rm{//}}\left( {SCD} \right).\)
b) Trong \(\left( {ABCD} \right)\) gọi \(K = AN \cap CD.\)
\[ \Rightarrow K \in AN;\,\,K \in CD.\]
Mà \(AN \subset \left( {AMN} \right)\) và \(CD \subset \left( {SCD} \right).\)
\( \Rightarrow K \in \left( {SCD} \right) \cap \left( {AMN} \right).\) (1)
Vì \(N\) là điểm trên cạnh \(BC\) sao cho \(BN = 2CN\) nên \(MN\) không song song với \(SC.\) Trong \(\left( {SBC} \right)\) gọi \[H = MN \cap SC.\]
\( \Rightarrow H \in MN;\,\,H \in SC.\)
Mà \(MN \subset \left( {AMN} \right)\) và \(SC \subset \left( {SCD} \right).\)
\( \Rightarrow H \in \left( {SCD} \right) \cap \left( {AMN} \right).\) (2)
Từ (1) và (2) ta có \(HK = \left( {SCD} \right) \cap \left( {AMN} \right).\)
Câu 2
\[\left( {BCE} \right){\rm{//}}\left( {DIK} \right).\]
\[\left( {ADF} \right){\rm{//}}\left( {BCE} \right).\]
\(\left( {BCE} \right){\rm{//}}\left( {BEJ} \right).\)
\[\left( {ADF} \right){\rm{//}}\left( {BEJ} \right).\]
Lời giải
Đáp án đúng là: B
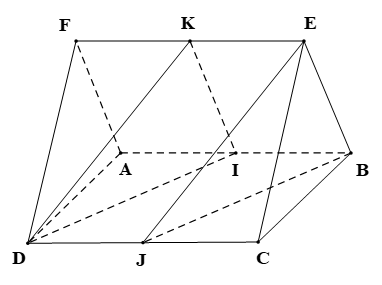
Do \(ABEF\) là hình bình hành nên \(AF{\rm{//}}BE.\)
Mà \(BE \subset \left( {BCE} \right);\,\,AF \not\subset \left( {BCE} \right) \Rightarrow AF{\rm{//}}\left( {BCE} \right).\)
Do \(ABCD\) là hình bình hành nên \(AD{\rm{//}}BC.\)
Mà \(BC \subset \left( {BCE} \right);\,\,AD \not\subset \left( {BCE} \right) \Rightarrow AD{\rm{//}}\left( {BCE} \right).\)
Ta có: \(AF{\rm{//}}\left( {BCE} \right);\,\,AD{\rm{//}}\left( {BCE} \right)\) và \(AF \cap AD = A\) trong \(\left( {ADF} \right).\)
Suy ra \[\left( {ADF} \right){\rm{//}}\left( {BCE} \right).\]
Câu 3
\(m \in \left\{ { - 4;\,\,1} \right\}.\)
\(m \in \left\{ { - 1;\,\,4} \right\}.\)
\(m \in \left\{ {0;\,\, - 3} \right\}.\)
\(m \in \left\{ {0;\,\,2} \right\}.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Điểm \(A'.\)
Điểm \(C'.\)
Điểm \(B'.\)
Điểm \(I'.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.