(1,0 điểm). Trong cuộc thi học sinh giỏi môn Toán lớp \(10\) có \(4\) học sinh tham gia với điểm đạt được của các học sinh là các số tự nhiên khác nhau không nhỏ hơn \(10\) và không lớn hơn \(20\). Biết rằng điểm trung bình, số trung vị của \(4\) học sinh trên đều bằng \(14\) và có khoảng biến thiên bằng \(4\). Xác định điểm thi của \(4\) học sinh trên.
(1,0 điểm). Trong cuộc thi học sinh giỏi môn Toán lớp \(10\) có \(4\) học sinh tham gia với điểm đạt được của các học sinh là các số tự nhiên khác nhau không nhỏ hơn \(10\) và không lớn hơn \(20\). Biết rằng điểm trung bình, số trung vị của \(4\) học sinh trên đều bằng \(14\) và có khoảng biến thiên bằng \(4\). Xác định điểm thi của \(4\) học sinh trên.
Quảng cáo
Trả lời:
Hướng dẫn giải
Giả sử điểm các học sinh đạt được lần lượt là \(a;\,b;\,c;\,d\,\left( {a < b < c < d} \right)\) và \(a,\,b,\,c,\,d \in \mathbb{N}\)
Ta có số trung vị: \({Q_2} = \frac{{b + c}}{2} = 14 \Rightarrow b + c = 28\)
Mà \(\overline x = 14 \Rightarrow a + b + c + d = 56 \Rightarrow a + d = 28\)
Ta có \(\left\{ {\begin{array}{*{20}{c}}{a < b < c}\\{b + c = 28}\end{array}} \right. \Rightarrow \left\{ {\begin{array}{*{20}{c}}{10 < b < 14}\\{2b < 28}\end{array}} \right.\) hay \(10 < b < 14\) mà \(b \in \mathbb{N} \Rightarrow b \in \left\{ {11;\,12;\,13} \right\}\)
+ Nếu \(b = 11\) thì \(c = 17\), mà \(10 \le a < b,a \in \mathbb{N} \Rightarrow a = 10;d = 18\)
Khi đó điểm các em đạt được lần lượt là \(10;\,\,\,11;\,\,\,17;\,\,18\)
+ Nếu \(b = 12\) thì \(c = 16\) mà \(10 \le a < b,a \in \mathbb{N} \Rightarrow \left[ \begin{array}{l}a = 10 \Rightarrow d = 18\\a = 11 \Rightarrow d = 17\end{array} \right.\)
Khi đó điểm các học sinh đạt được có thể là là: \(10;\,\,\,12;\,\,\,16;\,\,18\) hoặc \(11;\,\,\,12;\,\,\,16;\,\,\,17\).
+ Nếu \(b = 13\) thì \(c = 15\), mà \(10 \le a < b,a \in \mathbb{N} \Rightarrow \left[ \begin{array}{l}a = 10 \Rightarrow d = 18\\a = 11 \Rightarrow d = 17\\a = 12 \Rightarrow d = 16\end{array} \right.\)
Khi đó có ba mẫu số liệu thỏa đề bài có giá trị là: \(10;\,\,\,13;\,\,\,15;\,\,\,18\) hoặc \(11;\,\,\,13;\,\,\,15;\,\,\,17\) hoặc \(12;\,\,\,13;\,\,\,15;\,\,\,16\).
Vì khoảng biến thiên bằng \(4\) nên số điểm các em đạt được là: \(12;\,\,\,13;\,\,\,15;\,\,\,16\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Trọng tâm Lí, Hóa, Sinh 10 cho cả 3 bộ KNTT, CTST và CD VietJack - Sách 2025 ( 40.000₫ )
- Sách - Sổ tay kiến thức trọng tâm Vật lí 10 VietJack - Sách 2025 theo chương trình mới cho 2k9 ( 31.000₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
Lời giải
Hướng dẫn giải
Đáp án đúng là: A
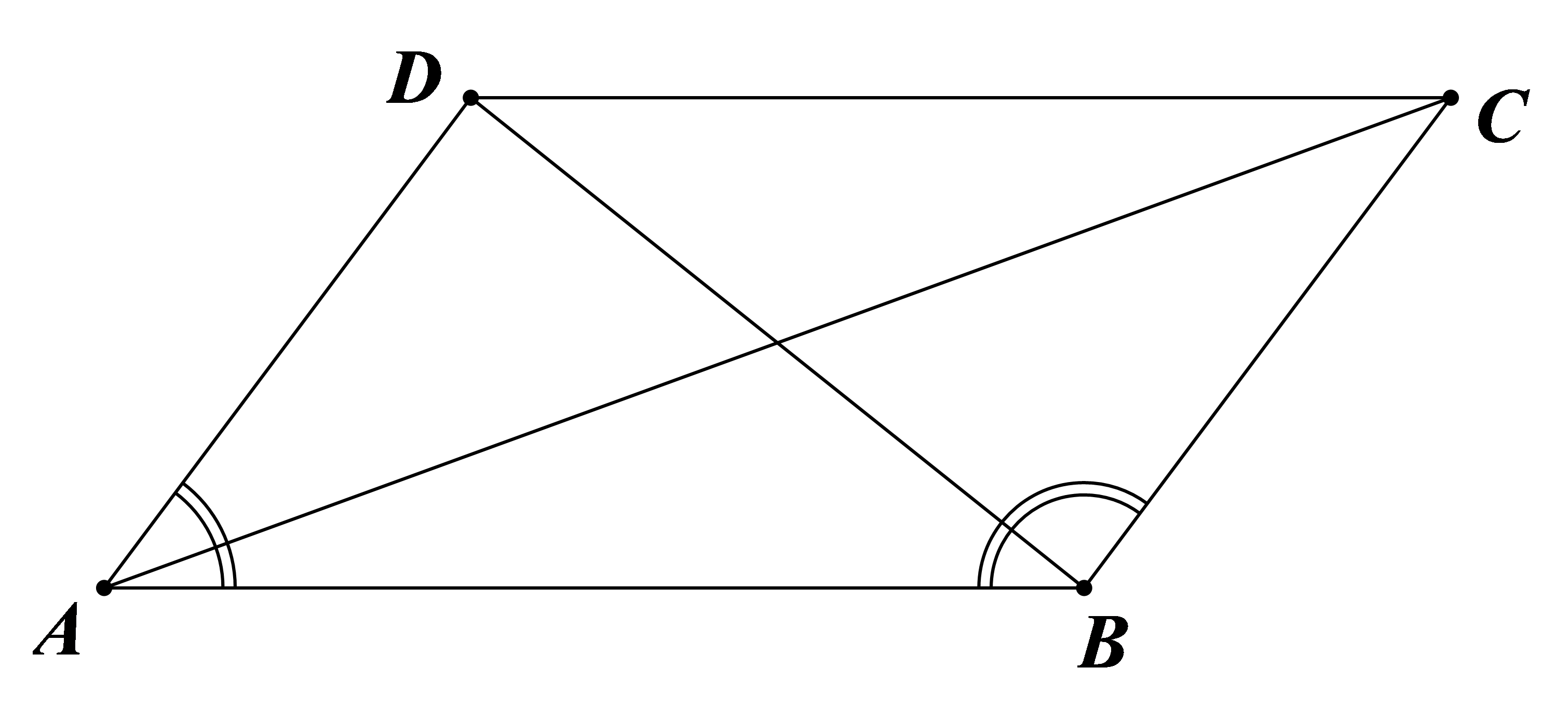
Theo giả thiết: \(\widehat {BAD} = 60^\circ \Rightarrow \widehat {ABC} = 120^\circ \).
\(\overrightarrow {BA} .\overrightarrow {BC} = \left| {\overrightarrow {BA} } \right|.\left| {\overrightarrow {BC} } \right|.\cos \left( {\overrightarrow {BA} ;\overrightarrow {BC} } \right) = AB.BC.\cos \widehat {ABC} = 2.1.\cos 120^\circ = - 1\).
Lời giải
Hướng dẫn giải
![Cho tam giác \[ABC\] đều có cạnh \(a\), điểm \ (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/11/39-1763537040.png)
a) Do \(M\) là trung điểm \(BC\) nên \(\overrightarrow {AM} = \frac{1}{2}\left( {\overrightarrow {AB} + \overrightarrow {AC} } \right)\) và \(AM\) là trung tuyến của tam giác \[ABC\].
Hơn nữa, \(G\) là trọng tâm của tam giác \[ABC\] nên \(\overrightarrow {AG} = \frac{2}{3}\overrightarrow {AM} \).
Do đó, \(\overrightarrow {AG} = \frac{2}{3}\overrightarrow {AM} = \frac{2}{3} \cdot \frac{1}{2}\left( {\overrightarrow {AB} + \overrightarrow {AC} } \right) = \frac{1}{3}\overrightarrow {AB} + \frac{1}{3}\overrightarrow {AC} \).
b) Ta có: \(\overrightarrow {AG} .\overrightarrow {AB} = \left( {\frac{1}{3}\overrightarrow {AB} + \frac{1}{3}\overrightarrow {AC} } \right).\overrightarrow {AB} = \frac{1}{3}{\overrightarrow {AB} ^2} + \frac{1}{3}\overrightarrow {AC} .\overrightarrow {AB} = \frac{1}{3}.{a^2} + \frac{1}{3}.a.a.{\rm{cos}}60^\circ \)
\( = \frac{1}{2}{a^2}\).
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
![Dây truyền đỡ trên cầu treo có dạng Parabol \(ACB\) như hình vẽ. Đầu, cuối của dây được gắn vào các điểm \(A,B\) trên mỗi trục \[AA,\,BB'\] với độ cao \(30m\). (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/11/38-1763537003.png)