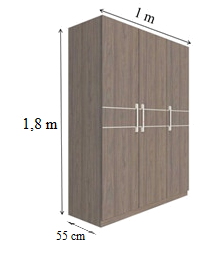
(1,0 điểm) Một xưởng sản xuất đồ nội thất muốn dùng để làm một chiếc tủ sản xuất tủ quần áo có kích thước như hình vẽ bên. Tính khoảng không gian bên trong tủ và diện tích gỗ xưởng cần như thiết kế đó.
Câu hỏi trong đề: Bộ 10 đề thi cuối kì 1 Toán 7 Cánh diều có đáp án !!
Quảng cáo
Trả lời:
Đổi \(55\,\,{\rm{cm}} = 0,55\,\,{\rm{m}}\).
Khoảng không gian bên trong chiếc tủ chính là thể tích của chiếc tủ và bằng \(1,8.1.0,55 = 0,99\,\,\left( {{{\rm{m}}^3}} \right)\).
Diện tích xung quanh chiếc tủ là: \[2.\left( {1 + 0,55} \right).1,8 = 5,58\,\,\left( {{{\rm{m}}^2}} \right)\].
Diện tích một mặt đáy tủ là: \(0,55.1 = 0,55\,\,\left( {{{\rm{m}}^2}} \right)\)
Diện tích gỗ cần dùng chính là diện tích tất cả các mặt của chiếc tủ và bằng: \(5,58 + 2.0,55 = 6,68\,\,\left( {{{\rm{m}}^2}} \right)\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Từ \(\frac{{a + b}}{{c + d}} = \frac{{b + c}}{{d + a}}\) suy ra \(\frac{{a + b}}{{b + c}} = \frac{{c + d}}{{d + a}}\)
Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
\[\frac{{a + b}}{{b + c}} = \frac{{c + d}}{{d + a}} = \frac{{a + b + c + d}}{{b + c + d + a}} = 1\]
Do đó \(a + b = b + c\) nên \(a = c\).
Lời giải
Gọi \(x,y,z\) lần lượt là số máy in của các phân xưởng thứ nhất, thứ hai, thứ ba.
Tổng số máy của ba phân xưởng là \(x + y + z = 57\).
Vì số ngày hoàn thành công việc tỉ lệ nghịch với số máy in nên ta có:
\(2x = 4y = 5z\) suy ra \(\frac{{2x}}{{20}} = \frac{{4y}}{{20}} = \frac{{5z}}{{20}}\) hay \(\frac{x}{{10}} = \frac{y}{5} = \frac{z}{4}\).
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
\(\frac{x}{{10}} = \frac{y}{5} = \frac{z}{4} = \frac{{x + y + z}}{{10 + 5 + 4}} = \frac{{57}}{{19}} = 3\)
Suy ra \(x = 3.10 = 30\); \(y = 3.5 = 15\); \(z = 3.4 = 12\).
Vậy số máy in của ba phân xưởng lần lượt là \(30;15;12\) (máy in).
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
(2,0 điểm) Cho hình vẽ biết \(xx' \bot tt'\), \[yy' \bot tt'\], \(\widehat {zCx'} = 110^\circ \), \(\widehat {CAO} = 50^\circ \), \(\widehat {OBy'} = 140^\circ \).
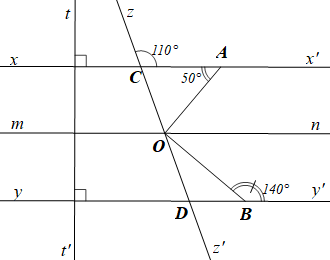
a) Vẽ lại hình (đúng số đo của các góc) và viết giả thiết, kết luận của bài toán.
b) Giải thích tại sao \(xx'\,{\rm{//}}\,yy'\).
c) Tìm số đo của \(\widehat {CDy}\).
d) Tìm số đo của \(\widehat {AOB}\).
(2,0 điểm) Cho hình vẽ biết \(xx' \bot tt'\), \[yy' \bot tt'\], \(\widehat {zCx'} = 110^\circ \), \(\widehat {CAO} = 50^\circ \), \(\widehat {OBy'} = 140^\circ \).

a) Vẽ lại hình (đúng số đo của các góc) và viết giả thiết, kết luận của bài toán.
b) Giải thích tại sao \(xx'\,{\rm{//}}\,yy'\).
c) Tìm số đo của \(\widehat {CDy}\).
d) Tìm số đo của \(\widehat {AOB}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.