(1,0 điểm) Quan sát biểu đồ sau:

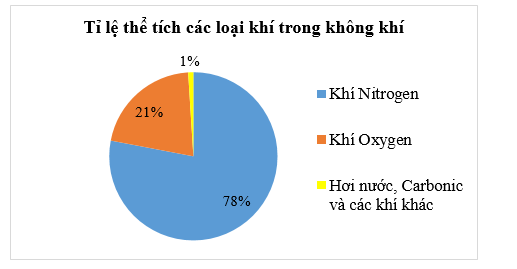
a) Lập bảng thống kê tỉ lệ thể tích các loại khí trong không khí.

b) Tính thể tích khí Oxygen trong một phòng trống hình hộp chữ nhật rộng \(15\,\,{{\rm{m}}^2}\) và cao \(4\,\,{\rm{m}}\).

 

a) Học sinh vẽ lại hình theo đúng số đo các góc.

b) Ta có \[\widehat {xAC} + \widehat {BAC} = 180^\circ \] (hai góc kề bù)

               \[\widehat {xAC} = 180^\circ - \widehat {BAC} = 180^\circ - 100^\circ = 80^\circ \]

Tia \(Ay\) là tia phân giác của \[\widehat {CAx}\] nên \(\widehat {xAy} = \widehat {CAy} = \frac{1}{2}\widehat {xAC} = 40^\circ \).

b) Ta có \[\widehat {CAy} = \widehat {ACB}\] (cùng bằng \[40^\circ \])

Mà hai góc này ở vị trí so le trong nên \(Ay\,{\rm{//}}\,BC\).

Do \(Ay\,{\rm{//}}\,BC\) nên \(\widehat {ABC} = \widehat {xAy} = 40^\circ \) (hai góc đồng vị).

Đáp án đúng là: C

Ta có \(\frac{{ - 3}}{{15}} = \frac{{ - 1}}{5}\). Phân số \(\frac{{ - 1}}{5}\) và \(\frac{{ - 1}}{{20}}\) là các phân số tối giản với mẫu số dương có ước nguyên tố là 2 và 5 nên viết được dưới dạng số thập phân hữu hạn.

Số \(\sqrt 3 \) là căn bậc hai số học của số 3, số 3 không phải số chính phương nên \(\sqrt 3 \) là số vô tỉ.

Số \(\frac{4}{{ - 12}} = \frac{{ - 1}}{3}\) là phân số tối giản với mẫu số dương có ước nguyên tố khác là 2 và 5 nên viết được dưới dạng số thập phân vô hạn tuần hoàn.