Giải các phương trình sau:
a) \(\left( {1 - 2x} \right)\left( {x + 5} \right) = 0.\)
b) \(\frac{2}{{{x^2} - 4}} - \frac{{x - 1}}{{x\left( {x - 2} \right)}} + \frac{{x - 4}}{{x\left( {x + 2} \right)}} = 0.\)
Giải các phương trình sau:
a) \(\left( {1 - 2x} \right)\left( {x + 5} \right) = 0.\)
b) \(\frac{2}{{{x^2} - 4}} - \frac{{x - 1}}{{x\left( {x - 2} \right)}} + \frac{{x - 4}}{{x\left( {x + 2} \right)}} = 0.\)
Quảng cáo
Trả lời:
Giải bởi Vietjack
a) \(\left( {1 - 2x} \right)\left( {x + 5} \right) = 0\)
\(1 - 2x = 0\) hoặc \(x + 5 = 0\)
\(2x = 1\) hoặc \(x = - 5\)
\(x = \frac{1}{2}\) hoặc \(x = - 5\)
Vậy phương trình đã cho có nghiệm là \(x = \frac{1}{2};\,\,x = - 5.\)b) Điều kiện xác định: \(x \ne 0,\,\,x \ne 2,\,\,x \ne - 2.\)
\(\frac{2}{{{x^2} - 4}} - \frac{{x - 1}}{{x\left( {x - 2} \right)}} + \frac{{x - 4}}{{x\left( {x + 2} \right)}} = 0\)
\(\frac{{2x}}{{x\left( {x - 2} \right)\left( {x + 2} \right)}} - \frac{{\left( {x - 1} \right)\left( {x + 2} \right)}}{{x\left( {x - 2} \right)\left( {x + 2} \right)}} + \frac{{\left( {x - 4} \right)\left( {x - 2} \right)}}{{x\left( {x - 2} \right)\left( {x + 2} \right)}} = 0\)
\(2x - \left( {x - 1} \right)\left( {x + 2} \right) + \left( {x - 4} \right)\left( {x - 2} \right) = 0\)
\(2x - \left( {{x^2} + 2x - x - 2} \right) + \left( {{x^2} - 2x - 4x + 8} \right) = 0\)
\(2x - \left( {{x^2} + x - 2} \right) + \left( {{x^2} - 6x + 8} \right) = 0\)
\(2x - {x^2} - x + 2 + {x^2} - 6x + 8 = 0\)
\( - 5x + 10 = 0\)
\( - 5x = - 10\)
\(x = 2\) (không thỏa mãn điều kiện).
Vậy phương trình đã cho vô nghiệm.Hot: 1000+ Đề thi cuối kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
Một ngân hàng đang áp dụng lãi suất gửi tiết kiệm kì hạn 12 tháng là \(5\% /\)năm. Bà Hoa dự định gửi một khoản tiền vào ngân hàng này để có số tiền lãi hàng năm ít nhất là 20 triệu đồng.
a) Gọi \(x\) (triệu đồng) là số tiền mà bà Hoa cần gửi tiết kiệm. Hãy viết bất phương trình phù hợp với dữ liệu đề bài.
b) Hỏi số tiền mà bà Hoa cần gửi tiết kiệm ít nhất là bao nhiêu?
Một ngân hàng đang áp dụng lãi suất gửi tiết kiệm kì hạn 12 tháng là \(5\% /\)năm. Bà Hoa dự định gửi một khoản tiền vào ngân hàng này để có số tiền lãi hàng năm ít nhất là 20 triệu đồng.
a) Gọi \(x\) (triệu đồng) là số tiền mà bà Hoa cần gửi tiết kiệm. Hãy viết bất phương trình phù hợp với dữ liệu đề bài.
b) Hỏi số tiền mà bà Hoa cần gửi tiết kiệm ít nhất là bao nhiêu?
Lời giải
a) Số tiền lãi bà Hoa thu được trong một năm là \(0,05x\) (triệu đồng).
Để có được số tiền lãi ít nhất là \(20\) triệu đồng/năm thì cần có: \(0,05x \ge 20\).
Vậy bất phương trình cần tìm là: \(0,05x \ge 20\).
b) Giải bất phương trình:
\(0,05x \ge 20\)
\(x \ge 400.\)
Vậy bà Hoa cần gửi ngân hàng ít nhất là \(400\) triệu đồng.
Lời giải
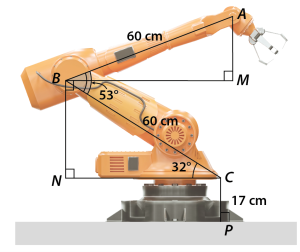
Xét \(\Delta BCN\) vuông tại \(N,\) ta có:
\(BN = BC \cdot \sin \widehat {BCN} = 60 \cdot \sin 32^\circ \approx 31,80{\rm{\;(cm)}}{\rm{.}}\)
Ta thấy \(NC\) và \(BM\) là các đoạn thẳng nằm trên phương ngang nên \(NC\,{\rm{//}}\,BM,\) suy ra \(\widehat {CBM} = \widehat {BCN} = 32^\circ \) (so le trong).
Khi đó, \(\widehat {ABM} = \widehat {ABC} - \widehat {CBM} = 53^\circ - 32^\circ = 21^\circ \).
Xét \(\Delta ABM\) vuông tại \(M\), ta có:
\(AM = AB \cdot \sin \widehat {ABM} = 60 \cdot \sin 21^\circ \approx 21,50\) (cm).
Vậy, độ cao của điểm \(A\) trên đầu cánh tay robot so với mặt đất là:
\(AM + BN + CP \approx 21,50 + 31,80 + 17 = 70,3\) (cm).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập