Câu hỏi:

26/11/2025 37

Cho $\Delta ABC$ vuông tại $A$ $\left( {AB < AC} \right)$.

a) Viết các tỉ số lượng giác của góc $B.$

b) Cho $AC = 16{\rm{\;cm}},\,\,BC = 20{\rm{\;cm}}.$ Giải tam giác $ABC$ (làm tròn số đo góc đến phút).

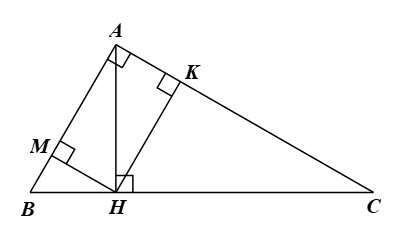
c) Kẻ đường cao $AH.$ Gọi $M$ là hình chiếu của $H$ lên $AB,$ $K$ là hình chiếu của $H$ lên $AC.$ Chứng minh rằng $BM + CK = BC\left( {{{\cos }^3}B + {{\sin }^3}B} \right).$

Xem lời giải

Câu hỏi trong đề: Bộ 5 đề thi giữa kì 1 Toán 9 Chân trời sáng tạo (Tự luận) có đáp án !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

a) Xét $\Delta ABC$ vuông tại $A,$ ta có:

$Cho $\Delta ABC$ vuông tại $A$ $\left( {AB < AC} \right)$. (ảnh 1)$

$\sin B = \frac{{AC}}{{BC}},\,\,\cos B = \frac{{AB}}{{BC}},$

$\tan B = \frac{{AC}}{{AB}},\,\,\cot B = \frac{{AB}}{{AC}}.$

b) Xét $\Delta ABC$ vuông tại $A,$ theo định lí Pythagore, ta có:

$B{C^2} = A{B^2} + A{C^2}$

Suy ra $A{B^2} = B{C^2} - A{C^2} = {20^2} - {16^2} = 144.$ Do đó $AB = 12{\rm{\;cm}}.$

Theo câu a, ta có: $\cos B = \frac{{AB}}{{BC}} = \frac{{12}}{{20}} = \frac{3}{5}.$ Từ đó suy ra $\widehat {B\,} \approx 53^\circ 8'.$

Lại có: $\widehat {B\,} + \widehat {C\,} = 90^\circ $, suy ra $\widehat {C\,} = 90^\circ - \widehat {B\,} \approx 90^\circ - 53^\circ 8' \approx 36^\circ 52'.$

Vậy $AB = 12{\rm{\;cm}},\,\,\widehat {B\,} \approx 53^\circ 8',\,\,\widehat {C\,} \approx 36^\circ 52'.$

c) Xét $\Delta ABH$ vuông tại $H,$ ta có: $\cos B = \frac{{BH}}{{AB}}.$

Xét $\Delta MBH$ vuông tại $M,$ ta có: $\cos B = \frac{{BM}}{{BH}}.$

Ta có: ${\cos ^3}B = \cos B \cdot \cos B \cdot \cos B = \frac{{AB}}{{BC}} \cdot \frac{{BH}}{{AB}} \cdot \frac{{BM}}{{BH}} = \frac{{BM}}{{BC}}.$

Chứng minh tương tự, ta cũng có: \[{\cos ^3}C = \cos C \cdot \cos C \cdot \cos C = \frac{{AC}}{{BC}} \cdot \frac{{CH}}{{AC}} \cdot \frac{{CK}}{{CH}} = \frac{{CK}}{{BC}}.\]

Lại có $\widehat {B\,} + \widehat {C\,} = 90^\circ $ nên $\cos C = \sin B,$ suy ra \[{\sin ^3}B = \frac{{CK}}{{BC}}.\]

Do đó ${\cos ^3}B + {\sin ^3}B = \frac{{BM}}{{BC}} + \frac{{CK}}{{BC}} = \frac{{BM + CK}}{{BC}}.$

Suy ra $BM + CK = BC\left( {{{\cos }^3}B + {{\sin }^3}B} \right).$

Hot: 1000+ Đề thi cuối kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Tại hai điểm cách nhau \[1\,\,{\rm{km}}\] trên mặt đất người ta nhìn thấy đỉnh núi với góc nâng lần lượt là \[40^\circ \] và \[32^\circ \] $(A,\,\,B,\,\,C$ thẳng hàng) (như hình vẽ). Tính chiều cao của ngọn núi (kết quả làm tròn đến chữ số thập phân thứ hai).

$Tại hai điểm cách nhau \[1\,\,{\rm{km}}\] trên mặt đất người ta nhìn thấy đỉnh núi với góc nâng lần lượt là \[40^\circ \] và \[32^\circ \] $(A,\,\,B,\,\,C$ thẳng hàng) (như hình vẽ). (ảnh 1)$

Xem đáp án

Lời giải

Đặt $BC = x\,\,\left( {{\rm{km}}} \right)$.

$Tại hai điểm cách nhau \[1\,\,{\rm{km}}\] trên mặt đất người ta nhìn thấy đỉnh núi với góc nâng lần lượt là \[40^\circ \] và \[32^\circ \] $(A,\,\,B,\,\,C$ thẳng hàng) (như hình vẽ). (ảnh 2)$

Khi đó $AC = BC + 1 = x + 1\,\,\left( {{\rm{km}}} \right).$

Xét \[\Delta ADC\] vuông tại \[C\] có

\[CD = BC \cdot \tan 40^\circ = x\tan 40^\circ & \left( 1 \right)\]

Xét \[\Delta BDC\] vuông tại \[C\] có

\[CD = AC \cdot \tan 32^\circ = \left( {x + 1} \right)\tan 32^\circ & \left( 2 \right)\]

Từ \[\left( 1 \right)\] và \[\left( 2 \right)\] suy ra \[x\tan 40^\circ = \left( {x + 1} \right)\tan 32^\circ \]

\[x\tan 40^\circ = x\tan 32^\circ + \tan 32^\circ \]

\[x\left( {\tan 40^\circ - \tan 32^\circ } \right) = \tan 32^\circ \]

\[x = \frac{{\tan 32^\circ }}{{\tan 40^\circ - \tan 32^\circ }} \approx 2,45\,\,\left( {{\rm{km}}} \right).\]

Vậy ngọn núi cao khoảng \[2,45{\rm{ km}}.\]

Câu 2

Trong cuộc thi “Đố vui để học”, mỗi thí sinh phải trả lời 12 câu hỏi. Mỗi câu hỏi gồm bốn phương án, trong đó chỉ có một phương án đúng. Với mỗi câu hỏi, nếu trả lời đúng thì được cộng thêm 5 điểm, trả lời sai bị trừ 2 điểm. Khi bắt đầu cuộc thi mỗi thí sinh có sẵn 20 điểm. Thí sinh nào đạt từ 50 điểm trở lên sẽ được vào vòng tiếp theo.

a) Gọi $x$ là số câu trả lời đúng $\left( {0 \le x \le 12,\,\,x \in \mathbb{N}} \right)$. Viết bất phương trình phù hợp với dữ liệu đề bài.

b) Hỏi thí sinh phải trả lời đúng ít nhất bao nhiêu câu thì được vào vòng thi tiếp theo?

Xem đáp án

Lời giải

a) Gọi $x$ là số câu trả lời đúng $\left( {0 \le x \le 12,\,\,x \in \mathbb{N}} \right)$.

Khi đó, số câu trả lời sai là $12 - x$ (câu hỏi).

Số điểm được cộng khi trả lời đúng $x$ câu hỏi là $5x$ (điểm)

Số điểm bị trừ khi trả lời đúng $12 - x$ câu hỏi là $2\left( {12 - x} \right)$ (điểm)

Khi bắt đầu cuộc thi mỗi thí sinh có sẵn 20 điểm nên số điểm thí

Theo đề bài, những thí sinh nào đạt từ 50 điểm trở lên sẽ được vào vòng tiếp theo nên ta có

$20 + 5x - 2\left( {12 - x} \right) \ge 50$

Vậy bất phương trình cần tìm là: $20 + 5x - 2\left( {12 - x} \right) \ge 50$.

b) Giải bất phương trình:

$20 + 5x - 2\left( {12 - x} \right) \ge 50$

$20 + 5x - 24 + 2x \ge 50$

$7x - 4 \ge 50$

$x \ge \frac{{54}}{7} \approx 7,714.$

Vậy thí sinh muốn vào vòng tiếp theo cần trả lời đúng 8 câu hỏi trở lên.

Câu 3