(0,5 điểm) Giải phương trình \(\cos \left( {3x - \frac{\pi }{6}} \right) = \frac{1}{2}\)
(0,5 điểm) Giải phương trình \(\cos \left( {3x - \frac{\pi }{6}} \right) = \frac{1}{2}\)
Quảng cáo
Trả lời:
ĐK: \(x \in \mathbb{R}\).
Ta có: \(\cos \left( {3x - \frac{\pi }{6}} \right) = \frac{1}{2} \Leftrightarrow \cos \left( {3x - \frac{\pi }{6}} \right) = \cos \left( {\frac{\pi }{3}} \right) \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{3x - \frac{\pi }{6} = \frac{\pi }{3} + k2\pi }\\{3x - \frac{\pi }{6} = - \frac{\pi }{3} + k2\pi }\end{array}} \right.,\left( {k \in \mathbb{Z}} \right)\) \( \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = \frac{\pi }{6} + \frac{{k2\pi }}{3}}\\{x = - \frac{\pi }{{18}} + \frac{{k2\pi }}{3}}\end{array}} \right.\,\,\,,\,\left( {k \in \mathbb{Z}} \right)\).
Vậy nghiệm của phương trình là: \(\left[ {\begin{array}{*{20}{c}}{x = \frac{\pi }{6} + \frac{{k2\pi }}{3}}\\{x = - \frac{\pi }{{18}} + \frac{{k2\pi }}{3}}\end{array}} \right.\,\,,\,\,\left( {k \in \mathbb{Z}} \right)\)
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Sách - Sổ tay kiến thức trọng tâm Vật lí 11 VietJack - Sách 2025 theo chương trình mới cho 2k8 ( 45.000₫ )
- Trọng tâm Hóa học 11 dùng cho cả 3 bộ sách Kết nối, Cánh diều, Chân trời sáng tạo VietJack - Sách 2025 ( 58.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
Lời giải
Chọn B
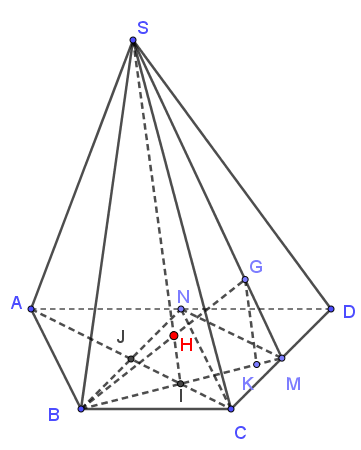
Gọi \(M\) là trung điểm của \(BC\). Chọn mặt phẳng \(\left( {SBM} \right) \supset BG\)
Trong mặt phẳng \(\left( {ABCD} \right)\), gọi \(I = BM \cap AC\) . Khi đó, \(\left( {SBM} \right) \cap \left( {SAC} \right) = SI\).
Trong mặt phẳng \(\left( {SBM} \right)\), \(H = BG \cap SI\).
Ta có: \(H \in SI\) mà \(SI \in \left( {SAC} \right)\) suy ra \(H \in \left( {SAC} \right)\)
\(H \in BG\)
Vậy \(H \in BG \cap \left( {SAC} \right)\).
Gọi \(N\) là trung điểm của \(AD\), suy ra \(MN\) là đường trung bình trong \(\Delta ACD\), suy ra \(MN\parallel AC\)
Ta có \(BC\parallel AN,BC = AN\) nên tứ giác \(ABCN\) là hình bình hành
Gọi \(J = AC \cap BN\), suy ra \(J\) là trung điểm của \(BN\).
Trong \(\Delta BMN\), ta có \(MN\parallel IJ\) và \(J\) là trung điểm của \(BM\) nên \(IB = IM\).
Trong mặt phẳng \(\left( {SBM} \right)\), kẻ \(GK\parallel SI\) với \(K \in BM\)
Xét \(\Delta SMI\), ta có \(GK\parallel SI\) nên \(\frac{{IM}}{{IK}} = \frac{{SM}}{{SG}} = \frac{3}{2}\)
Xét \(\Delta BGK\), ta có \(GK\parallel IH\) nên \(\frac{{HB}}{{HG}} = \frac{{BI}}{{IK}} = \frac{{IM}}{{IK}} = \frac{3}{2}\) (do \(IM = IK\)).
Lời giải
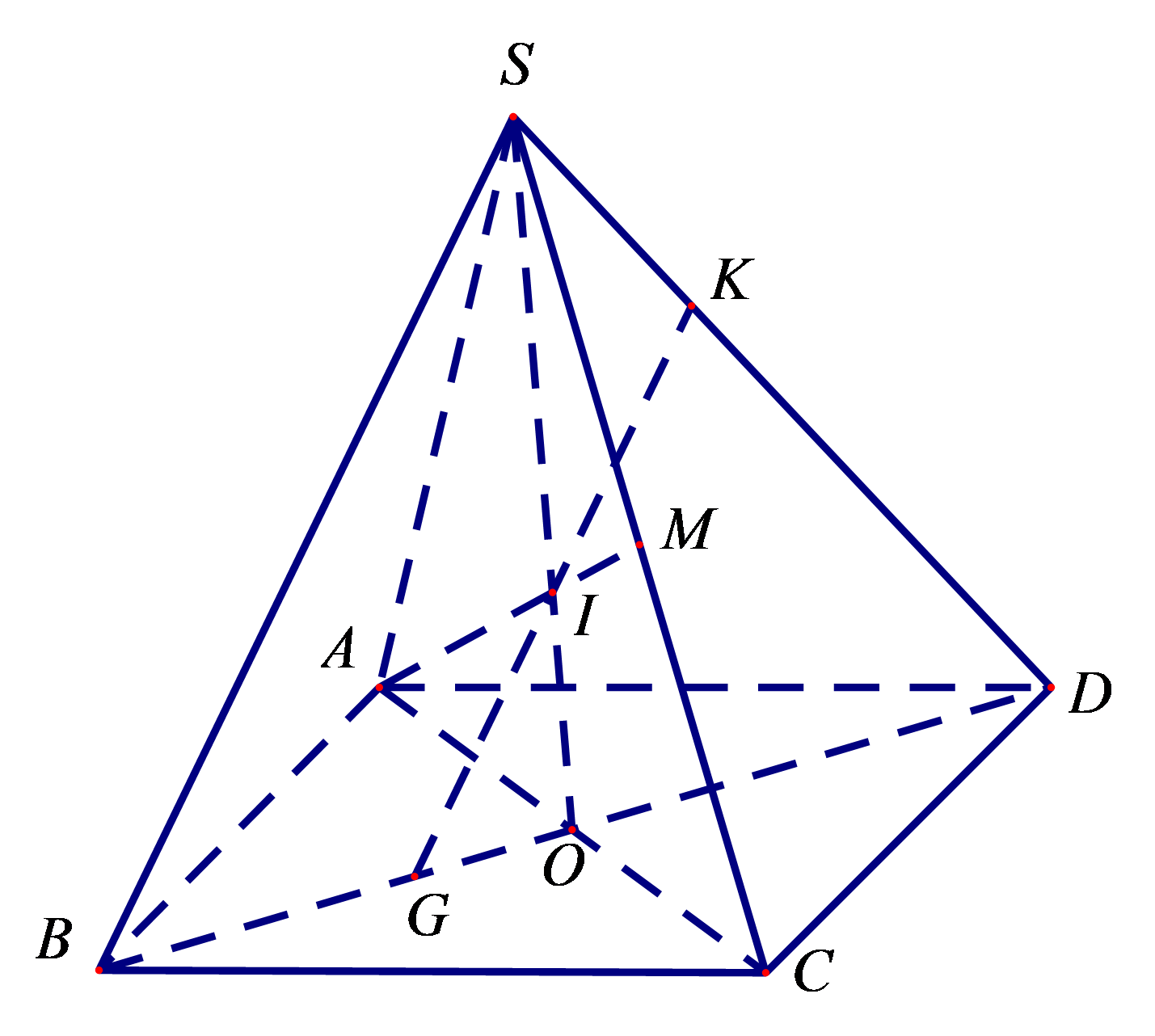
a. Ta có:\(S \in \left( {SAC} \right) \cap \left( {SBD} \right)\)
\(\left. {\begin{array}{*{20}{c}}{O \in AC \Rightarrow O \in \left( {SAC} \right)}\\{O \in BD \Rightarrow O \in \left( {SBD} \right)}\end{array}} \right\} \Rightarrow O \in \left( {SAC} \right) \cap \left( {SBD} \right)\). Vậy: \(\left( {SAC} \right) \cap \left( {SBD} \right) = SO\).
b. Ta có: \(\left. {\begin{array}{*{20}{c}}{M \in \left( {ABM} \right) \cap \left( {SCD} \right)}\\{AB\parallel CD}\\{AB \subset \left( {ABM} \right),CD \subset \left( {SCD} \right)}\\{\left( {ABM} \right) \cap \left( {SCD} \right) = {M_t}}\end{array}} \right\} \Rightarrow {M_t}\parallel AB\parallel CD\)
Trong \(\left( {SCD} \right)\) kẻ đường thẳng đi qua M, song song với \(CD\) và cắt \(SD\)tại \(N\).
Vậy: \(\left( {ABM} \right) \cap \left( {SCD} \right) = MN\).
c. Gọi \(O = AC \cap BD\), \(I = AM \cap SO\).
Trong mặt phẳng \(\left( {SBD} \right)\), kéo dài \(GI\) cắt \(SD\) tại \(K\)\( \Rightarrow K = SD \cap \left( {AMG} \right)\).
Tam giác \(SAC\) có \(SO\) và \(AM\) là hai đường trung tuyến.
Suy ra \(I\) là trọng tâm của tam giác \(SAC\) nên ta có \(\frac{{OI}}{{{\rm{O}}S}} = \frac{1}{3}\). (1)
Mặt khác, \(G\) là trọng tâm tam giác \(ABC\) nên có \(\frac{{OG}}{{OB}} = \frac{1}{3}\). (2)
Từ (1) và (2) suy ra \(\frac{{OI}}{{OS}} = \frac{{OG}}{{OB}}\)\( \Rightarrow GI{\rm{ // }}SB\)\( \Rightarrow GK{\rm{ // }}SB\).
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.