Người ta muốn mở rộng một mảnh vườn hình chữ nhật để có diện tích tăng lên 3 lần. Nhưng chiều rộng chỉ có thể tăng lên gấp đôi nên phải tăng thêm cả chiều dài. Khi đó vườn trở thành hình vuông. Hãy tính diện tích mảnh vườn sau khi mở rộng, biết chu vi mảnh vườn lúc đầu là 42m.
Người ta muốn mở rộng một mảnh vườn hình chữ nhật để có diện tích tăng lên 3 lần. Nhưng chiều rộng chỉ có thể tăng lên gấp đôi nên phải tăng thêm cả chiều dài. Khi đó vườn trở thành hình vuông. Hãy tính diện tích mảnh vườn sau khi mở rộng, biết chu vi mảnh vườn lúc đầu là 42m.
Câu hỏi trong đề: 5 bài tập Bài toán về hình chữ nhật, hình bình hành có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Hướng Dẫn Giải
Do chiều rộng tăng lên gấp 2 và diện tích tăng lên 3 lần. Nên chiều dài gấp lên số lần là: \(3:2 = \frac{3}{2}\) (lần)
Theo đề bài, thì sau khi tăng thì mảnh vườn thành hình vuông. Tức là ta có:
2 lần chiều rộng bằng \(\frac{3}{2}\) lần chiều dài.
Suy ra: chiều rộng bằng \(\frac{3}{2}:2 = \frac{3}{4}\) chiều dài.
Nửa chu vi mảnh vườn lúc đầu là: \(42:2 = 21{\rm{ (m)}}\)
Chiều rộng mảnh vườn lúc đầu là: \(21:(3 + 4) \times 3 = 9{\rm{ (m)}}\)
Cạnh mảnh vườn sau khi mở rộng là: \(9 \times 2 = 18{\rm{ (m)}}\)
Diện tích mảnh vườn sau khi mở rộng là: \(18 \times 18 = 324{\rm{ (}}{{\rm{m}}^2}{\rm{)}}\)
Đáp Số: 324 (m²)
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Hướng Dẫn Giải
Nửa chu vi hình chữ nhật là: \(170:2 = 85{\rm{ (m)}}\)
Phần diện tích bị giảm là hình chữ nhật có chiều dài là chiều rộng miếng đất và chiều rộng bằng 5m.
Chiều dài phần bị giảm hay chiều rộng mảnh đất là: \(170:5 = 34{\rm{ (m)}}\)
Chiều dài miếng đất là: \(85 - 34 = 51{\rm{ (m)}}\)
Diện tích miếng đất là: \(34 \times 51 = 1734{\rm{ (}}{{\rm{m}}^2}{\rm{)}}\)
Đáp Số: 1734 (m²)
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Hướng Dẫn Giải
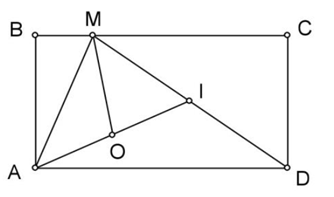
Ta có: \({S_{MAD}} = \frac{1}{2} \times AB \times AD\)
\({S_{ABM}} = \frac{1}{2} \times AB \times BM\); \({S_{DCM}} = \frac{1}{2} \times CD \times CM = \frac{1}{2} \times AB \times CM\)
=> \({S_{ABM}} + {S_{DCM}} = \frac{1}{2} \times AB \times BM + \frac{1}{2} \times AB \times CM = \frac{1}{2} \times AB \times (BM + CM)\)
\( = \frac{1}{2} \times AB \times BC = \frac{1}{2} \times AB \times AD = {S_{MAD}}\)
Mà \({S_{ABCD}} = ({S_{ABM}} + {S_{DCM}}) + {S_{MAD}}\) Nên \({S_{ABCD}} = 2 \times {S_{MAD}}\)
Lại có: \({S_{MAD}} = 2 \times {S_{MAI}}\) (chung chiều cao và đáy \(MI = MD:2\))
\( = 2 \times 2 \times {S_{MOI}} = 2 \times 2 \times 25 = 100{\rm{ (}}{{\rm{m}}^2}{\rm{)}}\)
Do đó: \({S_{ABCD}} = 2 \times 100 = 200{\rm{ (}}{{\rm{m}}^2}{\rm{)}}\)
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập