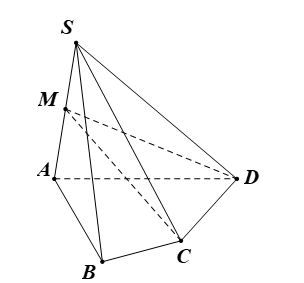
Cho hình chóp \(S.ABCD\) đáy là hình bình hành, \(G\)là trọng tâm tam giác \(SAC\). \(M\) là trung điểm của \(SD\)
a. Tìm giao điểm \(O\) của \(AC\) và \(\left( {SBD} \right)\)
b. Chứng minh rằng \(MO//\left( {SAB} \right)\)
c. \(\left( \alpha \right)\) chứa \(BM\) và song song với \(AC\), tìm giao tuyến của \(\left( \alpha \right)\) và \(\left( {SAC} \right)\)
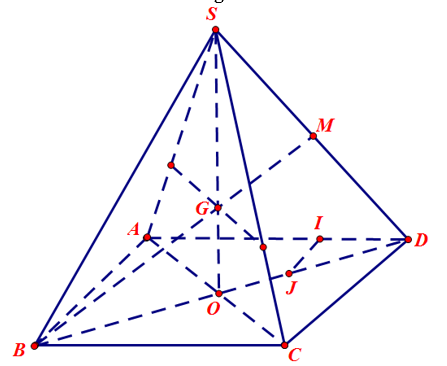
d. \(I\) trên đoạn \(AD\) sao cho \(\frac{{AI}}{{ID}} = 2\), \(J\) là trọng tâm tam giác \(ADC\).
Chứng minh rằng \(SC//\left( {GIJ} \right)\).
e. Điểm \(K\) di chuyển ở miền trong của hình bình hành \(ABCD\), kẻ \(KE\), \(KF\) lần lượt song song với \(SA,SB\) (Với \(E \in (SBC),\,F \in (SAD)\)). Tìm giá trị lớn nhất của \(\frac{{KE}}{{SA}}.\frac{{KF}}{{SB}}\).
Quảng cáo
Trả lời:
a. Trong \(\left( {ABCD} \right)\) gọi \(AC \cap BD = O\). Ta có
\(\begin{array}{l}O \in AC\\O \in BD \Rightarrow O \in (SBD)\end{array}\)
\( \Rightarrow \)\(O\) là giao điểm của \(AC\)và\((SBD)\)
b. \(MO\) là đường trung bình trong tam giác \(SBD\)\( \Rightarrow MO//SB\)
mà \(MO \not\subset (SAB) \Rightarrow MO//(SAB)\)
c. G là trọng tâm tam giác \(SAC\)\( \Rightarrow G\)là trọng tâm tam giác \(SBD\)
\( \Rightarrow G \in BM\)\( \Rightarrow G\)là điểm chung của \((\alpha )\) và \(\left( {SAC} \right)\)
Mà \((\alpha )//AC \Rightarrow \)giao tuyến của \((\alpha )\)và \(\left( {SAC} \right)\) là đường thẳng \(d\) qua \(G\) và song song với \(AC\)
d. Trong tam giác ABD có \(\frac{{DI}}{{IA}} = \frac{{DJ}}{{JB}} = \frac{1}{2} \Rightarrow IJ//AB \Rightarrow IJ//CD\)
mà \(IJ \not\subset (SCD)\)\( \Rightarrow IJ//(SCD)\)
Trong tam giác \(BMD\) có \(\frac{{MG}}{{GB}} = \frac{{DJ}}{{JB}} = \frac{1}{2} \Rightarrow JG//MD\) mà\(MG \not\subset (SCD),MD \subset (SCD) \Rightarrow MG//(SCD)\)
\(JG\) và \(IJ\) cắt nhau cùng nằm trong \(\left( {GIJ} \right)\) \( \Rightarrow \left( {JGI} \right)//(SCD)\)
\( \Rightarrow SC//(GIJ)\)
e.
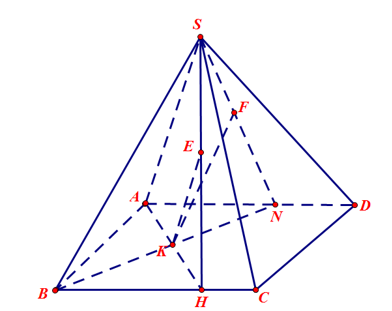
Trong \(\left( {ABCD} \right)\) gọi \(AK \cap BC = H\),vì \(KE//SA \Rightarrow E \in (SAH)\)mà \(E \in (SBC)\), \(SH\) là giao tuyến \(\left( {SAH} \right)\) và \(\left( {SBC} \right)\)\( \Rightarrow E \in SH\)
Trong tam giác \(SAH\) có \(\frac{{KE}}{{AS}} = \frac{{HK}}{{HA}}\)
Trong \(\left( {ABCD} \right)\) gọi \(BK \cap AD = N\),chứng minh tương tự ta có \(\frac{{KF}}{{BS}} = \frac{{NK}}{{NB}}\)
Mà \(\frac{{NK}}{{NB}} = \frac{{AK}}{{AH}} \Rightarrow \frac{{KE}}{{SA}} + \frac{{KF}}{{SB}} = \frac{{AK}}{{AH}} + \frac{{KH}}{{AH}} = 1\)
\( \Rightarrow \frac{{AK}}{{AH}}.\frac{{KH}}{{AH}} \le \frac{1}{4}{\left( {\frac{{AK}}{{AH}} + \frac{{KH}}{{AH}}} \right)^2} = \frac{1}{4}\). Dấu bằng xảy ra khi \(\frac{{AK}}{{AH}} = \frac{{KH}}{{AH}}\)
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Sách - Sổ tay kiến thức trọng tâm Vật lí 11 VietJack - Sách 2025 theo chương trình mới cho 2k8 ( 45.000₫ )
- Trọng tâm Hóa học 11 dùng cho cả 3 bộ sách Kết nối, Cánh diều, Chân trời sáng tạo VietJack - Sách 2025 ( 58.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
Lời giải
Chọn C
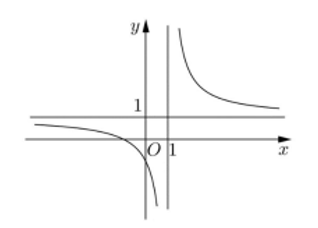
Xét \(f\left( x \right) = \frac{{{x^2} - 3x + 2}}{{x - 1}}\) có TXĐ \(D = \mathbb{R}\backslash \left\{ 1 \right\}\).
Hàm phân thức hữu tỉ liên tục trên TXĐ nên đáp án C thỏa mãn.
Câu 2
Lời giải
Chọn A
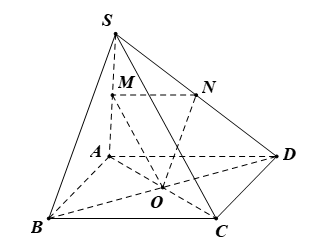
Ta có: \(\left\{ \begin{array}{l}MN//BC\\OM//SC\end{array} \right. \Rightarrow \left( {OMN} \right)//\left( {SBC} \right)\).
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.