Cô Lan có số tiền ban đầu 120 triệu đồng được gửi tiết kiệm với lãi suất năm không đổi là \(6{\rm{\% }}\).
Quảng cáo
Trả lời:
Công thức lãi kép theo định kì để tính tổng số tiền thu được \(A = P{\left( {1 + \frac{r}{n}} \right)^t}\), trong đó \(P\) là số tiền vốn ban đầu, \(r\) là lãi suất năm ( \(r\) cho dưới dạng số thập phân), \(n\) là số kì tính lãi trong một năm và \(t\) là số kì gửi.
Công thức lãi kép liên tục \(A = P{e^{rt}}\), ở đây \(r\) là lãi suất năm ( \(r\) cho dưới dạng số thập phân) và \(t\) là số năm gửi tiết kiệm.
Ta có: \(P = 120,r = 6{\rm{\% }} = 0,06,n = 4,t = 20\).
Thay vào công thức trên, ta được: \(A = 120{\left( {1 + \frac{{0,06}}{4}} \right)^{20}} = 120 \cdot 1,{015^{20}} \approx 161,623{\rm{\;}}\)( triệu đồng).
Ta có: \(P = 120,r = 6{\rm{\% }} = 0,06,n = 12,t = 60\). Thay vào công thức trên, ta được:
\(A = 120{\left( {1 + \frac{{0,06}}{{12}}} \right)^{60}} = 120 \cdot 1,{005^{60}} \approx 161,862{\rm{\;}}\) (triệu đồng)
Ta sử dụng công thức lãi kép liên tục \(A = P{e^{rt}}\), ở đây \(r\) là lãi suất năm ( \(r\) cho dưới dạng số thập phân) và \(t\) là số năm gửi tiết kiệm.
Ta có: \(P = 120,r = 6{\rm{\% }} = 0,06,t = 5\) nên \(A = 120 \cdot {\theta ^{0,06 \cdot 5}} = 120 \cdot {\theta ^{0,3}} \approx 161,983{\rm{\;}}\)(triệu đồng).
Ta có phương trình: \(180 = 120.{e^{rt}}\)ó\(2{e^{0.06t}} = 3\)
Lấy logarit tự nhiên của hai vế của phương trình, ta có: \(0.06t = \ln (1.5)\)
Do đó, \(t = \frac{{\ln (1.5)}}{{0.06}} \approx 11.55\) năm.
Vậy thời gian cần để cô Lan thu được số tiền là 150 triệu đồng nếu gửi theo thể thức lãi kép liên tục là khoảng 11.55 năm.
a) Đúng: Số tiền (cả vốn lẫn lãi) cô Lan thu được sau 5 năm nếu được tính lãi kép theo thể thức tính lãi hàng quý là khoảng \(161,623\) triệu đồng.
b) Đúng: Số tiền (cả vốn lẫn lãi) cô Lan thu được sau 5 năm nếu được tính lãi kép theo thể thức tính lãi hàng tháng là khoảng \(161,862{\rm{\;}}\) triệu đồng.
c) Sai: Số tiền (cả vốn lẫn lãi) cô Lan thu được sau 5 năm nếu được tính lãi kép theo thể thức tính lãi liên tục là khoảng \(161,983\) triệu đồng.
d) Sai: Thời gian cần thiết để cô Lan thu được số tiền cả vốn lẫn lãi là 180 triệu đồng nếu gửi theo thể thức lãi lép liên tục khoảng \(11,55\)năm.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Trọng tâm Sử, Địa, GD KTPL 11 cho cả 3 bộ Kết nối, Chân trời, Cánh diều VietJack - Sách 2025 ( 38.000₫ )
- Sách - Sổ tay kiến thức trọng tâm Vật lí 11 VietJack - Sách 2025 theo chương trình mới cho 2k8 ( 45.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
Lời giải
a) Đúng: Hàm số \(y = {\log _{\frac{{2024}}{{2023}}}}x\) có tập giá trị là \(\mathbb{R}\).
b) Sai: Vì cơ số \(\frac{{2023}}{{2024}} \in \left( {0\,;\,1} \right)\) nên hàm số \(y = {\left( {\frac{{2023}}{{2024}}} \right)^x}\) nghịch biến trên \(\mathbb{R}\).
c) Đúng: Hàm số \(y = {\log _{\frac{{2024}}{{2023}}}}x\) có tập xác định là \(\left( {0\,;\, + \infty } \right)\) nên có đồ thị nằm bên phải trục tung.
d) Sai: Vì \({\left( {\frac{{2023}}{{2024}}} \right)^x} > 0,\,\forall x \in \mathbb{R}\) nên đồ thị hàm số \(y = {\left( {\frac{{2023}}{{2024}}} \right)^x}\) không cắt trục tung.
Câu 2
Lời giải
Chọn B
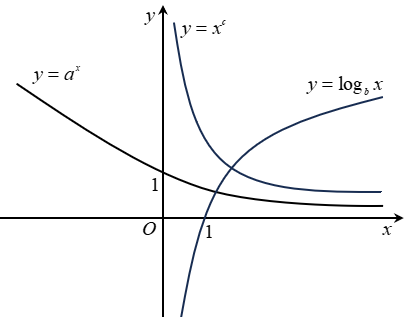
Ta thấy đồ thị \(y = {x^c}\)đi xuống nên \(c < 0\), đồ thị \(y = {a^x}\)đi xuống nên \(0 < a < 1\), đồ thị \(y = {\log _b}x\) đi lên nên \(b > 1.\)
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.