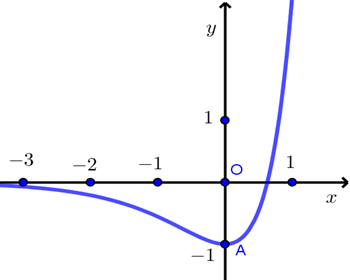
Gọi \(M\left( {{x_0};{y_0}} \right)\) là điểm trên đồ thị hàm số \(y = {x^3} - 3{x^2} - 1\) mà tiếp tuyến tại đó có hệ số góc bé nhất trong các tiếp tuyến của đồ thị hàm số. Khi đó \(x_0^2 + y_0^2\) bằng bao nhiêu?
Quảng cáo
Trả lời:
Trả lời: 10
Lời giải
Ta có \(y' = 3{x^2} - 6x\)
Suy ra hệ số góc \(k = 3x_0^2 - 6{x_0}\)
Ta có \(3x_0^2 - 6{x_0} \ge - 3\) suy ra \({k_{\min }} = - 3\) khi \({x_0} = 1\).
Từ đó suy ra \({y_0} = - 3\)
Vậy \(x_0^2 + y_0^2 = {1^2} + {\left( { - 3} \right)^2} = 10\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Sách - Sổ tay kiến thức trọng tâm Vật lí 11 VietJack - Sách 2025 theo chương trình mới cho 2k8 ( 45.000₫ )
- Trọng tâm Hóa học 11 dùng cho cả 3 bộ sách Kết nối, Cánh diều, Chân trời sáng tạo VietJack - Sách 2025 ( 58.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
a) \(x = \frac{{3a}}{4}\).
b)\(y = 2x\).
c) \(y = z + x\).
Lời giải
|
a) Sai |
b) Đúng |
c) Sai |
d) Đúng |
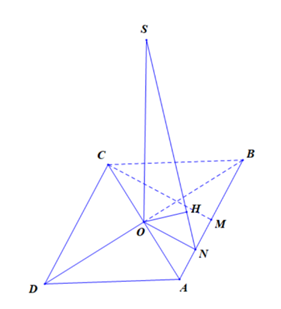
Tam giác \(ABC\) đều cạnh \(a\) nên đường cao \(CM = \frac{{a\sqrt 3 }}{2}\). Gọi \(N\) là trung điểm của \(AM\) \( \Rightarrow ON \bot AB;ON = \frac{{a\sqrt 3 }}{4}\).
Kẻ \(OH \bot SN\)\( \Rightarrow d\left( {O,\left( {SAB} \right)} \right) = OH\).
\[\frac{1}{{O{H^2}}} = \frac{1}{{S{O^2}}} + \frac{1}{{O{N^2}}}\]; \[ON = \frac{1}{2}CM = \frac{{a\sqrt 3 }}{4}\]; \[SO = \frac{{3a}}{4} \Rightarrow OH = \frac{{3a}}{8}\].
\(x = d\left( {O,\left( {SAB} \right)} \right) = \frac{{3a}}{8}\), \(y = d\left( {D,\left( {SAB} \right)} \right) = 2.d\left( {O,\left( {SAB} \right)} \right) = 2x\), \(z = d\left( {CD,SA} \right)\)\( = d\left( {D,\left( {SAB} \right)} \right) = 2x\).
Vậy \(x + y + z = 5x = \frac{{15a}}{8}\).
Lời giải
Trả lời: \( \approx {51,14^^\circ }\)
Lời giải
Trong mặt phẳng \(\left( {{A^\prime }{B^\prime }{C^\prime }{D^\prime }} \right)\), kẻ \({A^\prime }H \bot {B^\prime }{D^\prime }\) tại \(H\).
Ta có: \(\left\{ {\begin{array}{*{20}{l}}{{B^\prime }{D^\prime } \bot {A^\prime }H}\\{{B^\prime }{D^\prime } \bot A{A^\prime }\left( {{\rm{do }}A{A^\prime } \bot \left( {{A^\prime }{B^\prime }{C^\prime }{D^\prime }} \right)} \right)}\end{array} \Rightarrow {B^\prime }{D^\prime } \bot \left( {A{A^\prime }H} \right) \Rightarrow {B^\prime }{D^\prime } \bot AH} \right.\).
Do đó \(\widehat {AH{A^\prime }}\) là góc phẳng nhị diện \(\left[ {A,{B^\prime }{D^\prime },{A^\prime }} \right]\).
![Một hộp phấn không bụi có dạng hình hộp chữ nhật, chiều cao hộp phấn bằng 8,2cm và đáy của nó có hai kích thước là 8,5cm;10,5cm (xem hình vẽ sau). Tìm góc phẳng nhị diện [A,B'D',A'] (ảnh 2)](https://video.vietjack.com/upload2/quiz_source1/2025/12/blobid6-1765851742.png)
Tam giác \({A^\prime }{B^\prime }{D^\prime }\) vuông tại \({A^\prime }\) có đường cao \({A^\prime }H\) nên
\(\frac{1}{{{A^\prime }{H^2}}} = \frac{1}{{{A^\prime }{B^{\prime 2}}}} + \frac{1}{{{A^\prime }{D^{\prime 2}}}} \Rightarrow {A^\prime }H = \frac{{{A^\prime }{B^\prime } \cdot {A^\prime }{D^\prime }}}{{\sqrt {{A^\prime }{B^{\prime 2}} + {A^\prime }{D^{\prime 2}}} }} = \frac{{357}}{{2\sqrt {730} }}{\rm{. }}\)
Tam giác \(AH{A^\prime }\) vuông tại \({A^\prime }\) có:
\(\tan \widehat {AH{A^\prime }} = \frac{{A{A^\prime }}}{{{A^\prime }H}} = \frac{{8,2}}{{\frac{{357}}{{2\sqrt {730} }}}} \Rightarrow \widehat {AH{A^\prime }} \approx {51,14^^\circ }\)
Câu 3
a) Ta có \[\mathop {\lim }\limits_{x \to 1} \frac{{{x^2} - 1}}{{x - 1}} = 2\]
b) Với \(a = - 2\) thì hàm số có đạo hàm tại \[x = 1\]
c) Với \(a = 2\) thì hàm số có đạo hàm tại \[x = 1\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
a) Xác suất để chọn được 1 học sinh nam ở trường không thuận tay trái là: \(\frac{{273}}{{800}}{\rm{. }}\)
b) Xác suất để chọn được 1 học sinh nữ ở trường không thuận tay trái là: \(\frac{{89}}{{160}}{\rm{. }}\)
c) Xác suất để chọn được 1 học sinh nam, 1 học sinh nữ ở trường thuận tay trái lần lượt là: \(\frac{{11}}{{160}}{\rm{ v\`a }}\frac{{27}}{{800}}{\rm{. }}\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
a) Đường thẳng \(y = 0\) cắt đồ thị hàm số \(\left( C \right)\) tại điểm có hoành độ là \(x = {\log _3}2\).
b) Bất phương trình \(f\left( x \right) \ge - 1\) có nghiệm duy nhất.
c) Bất phương trình \(f\left( x \right) \ge 0\) có tập nghiệm là: \(\left( { - \infty ;{{\log }_3}2} \right)\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
![Một hộp phấn không bụi có dạng hình hộp chữ nhật, chiều cao hộp phấn bằng 8,2cm và đáy của nó có hai kích thước là 8,5cm;10,5cm (xem hình vẽ sau). Tìm góc phẳng nhị diện [A,B'D',A'] (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/12/blobid7-1765851756.png)