Cho hình chóp \(S.ABC\) có đáy \(ABC\) là tam giác vuông tại \(B\), \(AB = a,BC = a\sqrt 3 \). Hình chiếu vuông góc của \(S\) trên mặt đáy là trung điểm \(H\) của cạnh \(AC\). Biết \(SB = a\sqrt 2 \).Khoảng cách từ điểm \(H\) đến mặt phẳng \(\left( {SAB} \right)\) bằng:………….
Quảng cáo
Trả lời:
Giải bởi Vietjack
Dựng \(HI \bot AB\).
Ta có: \[\left. \begin{array}{l}AB \bot IH\\AB \bot SH\end{array} \right\} \Rightarrow AB \bot \left( {SIH} \right)\] và \(\left( {SIH} \right) \cap \left( {SAB} \right) = SI\).
Dựng \(HK \bot SI\).
Ta có : \[\left. \begin{array}{l}HK \bot AB\\HK \bot SI\end{array} \right\} \Rightarrow HK \bot \left( {SAB} \right)\].
Vậy \(d\left( {H,\left( {SAB} \right)} \right) = HK\).
Do \(HI/{\kern 1pt} /BC\) nên dễ dàng chỉ ra được \(I\) là trung điểm của \(AB\) và \(IH = \frac{{BC}}{2} = \frac{{a\sqrt 3 }}{2}\), \(IA = IB = \frac{{AB}}{2} = \frac{a}{2}\).
Ta có \(AB \bot SI\) nên \(SI = \sqrt {S{B^2} - I{B^2}} = \sqrt {2{a^2} - \frac{{{a^2}}}{4}} = \frac{{a\sqrt 7 }}{2}\).
Do \(SH \bot IH\) nên xét tam giác vuông \(SIH\) có:
\(SH = \sqrt {S{I^2} - I{H^2}} = \sqrt {\frac{{7{a^2}}}{4} - \frac{{3{a^2}}}{4}} = a\); \(HK = \frac{{SH.HI}}{{SI}} = \frac{{a.\frac{{a\sqrt 3 }}{2}}}{{\frac{{a\sqrt 7 }}{2}}} = \frac{{a\sqrt {21} }}{7}\).
Do vậy, ta có \(d\left( {H,\left( {SAB} \right)} \right) = \frac{{a\sqrt {21} }}{7}\).
Hot: 1000+ Đề thi cuối kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Các sản phẩm khác của Vietjack:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Theo giả thiết ta có \[P\left( 1 \right) = X = 253\].
Ngày thứ 10 có 2024 ca nên \(P\left( {10} \right) = X.{{\rm{e}}^{9{r_0}}} \Leftrightarrow 2024 = 253.{{\rm{e}}^{9{r_0}}} \Leftrightarrow {r_0} = \frac{{\ln 8}}{9}\).
Vậy ngày thứ 20 số ca nhiễm bệnh là \(P\left( {20} \right) = 253.{{\rm{e}}^{\frac{{19\ln 8}}{9}}} \approx 20401.\)
Lời giải
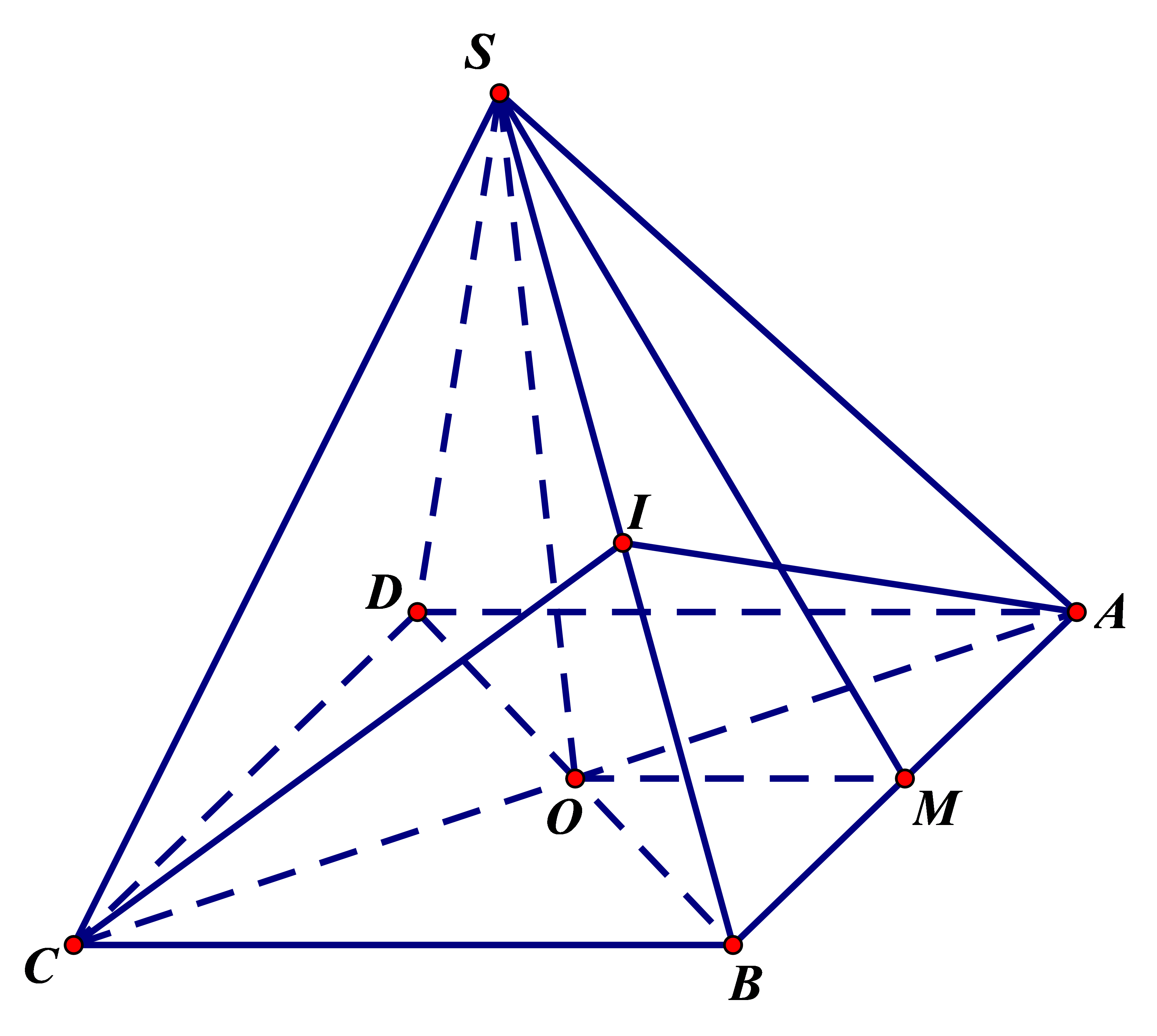
+ Gọi hình chóp tứ giác đều là \(S.ABCD\) như hình vẽ, \(O = AC \cap BD,\,M\) là trung điểm của \(AB\)
Khi đó góc nhị diện tạo bởi mặt bên \(\left( {SAB} \right)\) và mặt đáy \(\left( {ABCD} \right)\) là \(\left[ {S,AB,O} \right]\).
Ta có \(SM \bot AB\) và \(OM \bot AB\), suy ra \(\widehat {SMO}\) là góc phẳng nhị diện \(\left[ {S,AB,O} \right]\).
Xét tam giác \(SMO\) ta có \[\tan \widehat {SMO} = \frac{{SO}}{{OM}} \Rightarrow BC = 2OM = \frac{{2SO}}{{\tan \widehat {SMO}}} \approx 230,36\,(m)\]
+ Tìm số đo của góc phẳng nhị diện hai mặt bên, tức là số đo của góc phẳng nhị diện \(\left[ {A,SB,C} \right]\)
Kẻ \(AI \bot SB\), lại có \(SB \bot AC\)(vì\(AC \bot \left( {SBD} \right)\)) từ đó suy ra \(SB \bot CI\).
Vậy góc phẳng nhị diện \(\left[ {A,SB,C} \right]\) là góc \(\widehat {AIC}\).
Hai tam giác \(\Delta SAB = \Delta SBC\) suy ra hai đường cao \(AI = CI\), tam giác \(\Delta IAC\) cân tại I.
Đặt \(a = 230,36;\,h = 146,6\)
Ta có \(AC = a\sqrt 2 \Rightarrow OA = \frac{{a\sqrt 2 }}{2} \Rightarrow SA = \sqrt {S{O^2} + O{A^2}} = \sqrt {{h^2} + \frac{{{a^2}}}{2}} \); \[SM = \sqrt {S{O^2} + O{M^2}} = \sqrt {{h^2} + \frac{{{a^2}}}{4}} \]
Trong tam giác cân SAB ta có \({S_{\Delta SAB}} = \frac{1}{2}AI.SB = \frac{1}{2}SM.AB \Rightarrow AI = \frac{{SM.AB}}{{SB}} = \frac{{\sqrt {{h^2} + \frac{{{a^2}}}{4}} .a}}{{\sqrt {{h^2} + \frac{{{a^2}}}{2}} }}\)
\(\cos \widehat {AIC} = \frac{{A{I^2} + C{I^2} - A{C^2}}}{{2AI.CI}} = \frac{{2{a^2}\left( {\frac{{4{h^2} + {a^2}}}{{2\left( {2{h^2} + {a^2}} \right)}}} \right) - 2{a^2}}}{{2.\frac{{4{h^2} + {a^2}}}{{2\left( {2{h^2} + {a^2}} \right)}}{a^2}}} = \frac{{ - {a^2}}}{{4{h^2} + {a^2}}}\), thay số \(a = 230,36;\,h = 146,6\)
Ta suy ra được \(\widehat {AIC} \approx {112^0}26'16''\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. 1.
B. 2.
C. 3.
D. Vô số.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. \(m + n = 9\).
B. \(m + n = - 7\).
C. \(m + n = 30\).
D. \(m + n = 31\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. \({a^m}.{a^n} = {a^{m.n}}\).
B. \({\left( {a.b} \right)^m} = {a^m}.{b^m}\).
C. \({a^m} + {a^n} = {a^{m + n}}\).
D. \({a^m}.{b^n} = {\left( {a.b} \right)^{m + n}}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập