Trong mặt phẳng toạ độ \(Oxy\), cho tam giác \(ABC\) cân tại \(A\) biết đỉnh \(A\left( {6;6} \right)\). Đường thẳng \(d\) đi qua trung điểm các cạnh \(AB,\,AC\) có phương trình \(x + y - 4 = 0\). Biết điềm \(E\left( {1;\, - 3} \right)\) thuộc đường cao đi qua đỉnh \(C\) của tam giác \(ABC\). Giả sử \(C\left( {{x_C};\,{y_C}} \right)\) và \({x_C} > 0\). Tính \(x_C^2 + y_C^2\)

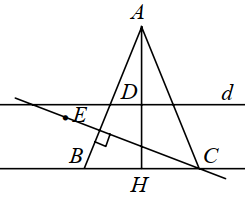
Ta có: \(AH \bot d \Rightarrow \) phương trình đường thẳng \(AH:x - y = 0\).

Gọi \(H,\,D\) lần lượt là trung điểm của \(BC,\,AH\).

Toạ độ \(D\) là nghiệm của hệ: \(\left\{ \begin{array}{l}x + y - 4 = 0\\x - y = 0\end{array} \right. \Leftrightarrow x = y = 2\). Vậy \(D\left( {2;\,2} \right) \Rightarrow H\left( { - 2; - 2} \right)\).

Do \(BC//d \Rightarrow BC\) có phương trình: \(x + y + 4 = 0\).

\(C \in BC \Rightarrow C\left( {t;\, - t - 4} \right)\) với \(t > 0\). Do \(H\) là trung điểm \(BC\) nên suy ra \(B\left( { - t - 4;\,t} \right)\).

Ta có \(\overrightarrow {AB} .\overrightarrow {CE}  = 0 \Leftrightarrow {t^2} + 2t - 8 = 0 \Rightarrow t = 2\) (do \(t > 0\)).

Vậy \(C\left( {2;\, - 6} \right)\) nên \(x_C^2 + y_C^2 = {2^2} + {\left( { - 6} \right)^2} = 40\).