Trong không gian\(Oxyz\), mặt phẳng cắt ba trục toa độ tại ba điểm \(D(3;0;0)\), \(E(0; - 2;0),G(0;0; - 7)\) có phương trình chính tắc là:
Câu hỏi trong đề: Bộ 10 đề thi cuối kì 2 Toán 12 Cánh diều có đáp án !!
Quảng cáo
Trả lời:
Đáp án đúng là: C
Phương trình mặt chắn là: \(\frac{x}{3} - \frac{y}{2} - \frac{z}{7} = 1\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Trả lời: 4
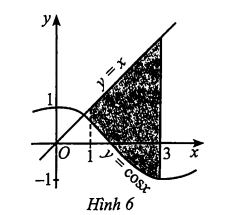
Hình phẳng đã cho được giới hạn bởi các đồ thị hàm số \(y = \cos x,\,y = x\) và hai đường thẳng \(x = 1,\,x = 3\). Khi đó diện tích hình phẳng được tính theo công thức
\(S = \int\limits_1^3 {\left| {\cos x - x} \right|{\rm{d}}x} \). Vì \(x \ge \cos x,\,\forall x \in \left[ {1;3} \right]\) nên ta có:
\(S = \int\limits_1^3 {\left( {x - \cos x} \right){\rm{d}}x} = \left. {\left( {\frac{{{x^2}}}{2} - \sin x} \right)} \right|_1^3 = 4 - \sin 3 + \sin 1 \approx 4\).
Câu 2
Lời giải
Đáp án đúng là: B
Do \[\int {f\left( t \right)dt} = \int {{{480.2}^t}\ln 2{\rm{ }}dt} = 480.\ln 2.\frac{{{2^t}}}{{\ln 2}} + C = {480.2^t} + C = F(t)\].
Biết tại thời điểm bắt đầu quan sát, số lượng cá thể được ước tính một cách chính xác khoảng 480 cá thể nên
\[F(0) = {480.2^0} + C = 480 \Rightarrow C = 0\]. Suy ra \[F\left( t \right) = {480.2^t}\].
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.