Trong một đợt kiểm tra sức khoẻ, có một loại bệnh X mà tỉ lệ người mắc bệnh là \(0,2\% \) và một loại xét nghiệm Y mà ai mắc bệnh X khi xét nghiệm Y cũng có phản ứng dương tính. Tuy nhiên, có \(6\% \) những người không bị bệnh X lại có phản ứng dương tính với xét nghiệm Y. Chọn ngẫu nhiên 1 người trong đợt kiểm tra sức khoẻ đó. Giả sử người đó có phản ứng dương tính với xét nghiệm Y. Xác suất người đó bị mắc bệnh X là bao nhiêu (làm tròn kết quả đến hàng phần trăm)?
Câu hỏi trong đề: Bộ 10 đề thi cuối kì 2 Toán 12 Cánh diều có đáp án !!
Quảng cáo
Trả lời:
Đáp án đúng là: B
Xét các biến cố:
\(A:\) "Người được chọn mắc bệnh X";
B: "Người được chọn có phản ứng dương tính với xét nghiệm Y".
Theo giả thiết ta có: \(P\left( A \right) = 0,002;\;\;P\left( {\bar A} \right) = 1 - 0,002 = 0,998\);
\(P\left( {B\mid A} \right) = 1;\;\;P\left( {B\mid \bar A} \right) = 0,06\).
Theo công thức Bayes, ta có:
\(P\left( {A\mid B} \right) = \frac{{P\left( A \right).P\left( {B\mid A} \right)}}{{P\left( A \right).P\left( {B\mid A} \right) + P\left( {\bar A} \right).P\left( {B\mid \bar A} \right)}} = \frac{{0,002.1}}{{0,002.1 + 0,998.0,06}} \approx 0,03\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- 250+ Công thức giải nhanh môn Toán 12 (chương trình mới) ( 18.000₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Trả lời: 4,5
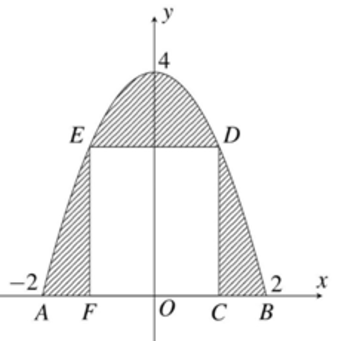
Vì chiều cao của cổng bằng 4 m nên \(\left( P \right):y = a{x^2} + 4\).
Mà \(\left( {2;0} \right) \in \left( P \right)\) nên \(0 = a{.2^2} + 4 \Leftrightarrow a = - 1\). Do đó \(y = - {x^2} + 4\).
Do đó diện tích toàn bộ chiếc cổng là \(S = \int\limits_{ - 2}^2 {\left| { - {x^2} + 4} \right|} dx = \frac{{32}}{3}\).
Vì \(D \in \left( P \right)\) nên \(D\left( {a; - {a^2} + 4} \right),\left( {0 < a < 2} \right)\).
Suy ra \(FC = 2a;CD = 4 - {a^2}\). Do đó \({S_{CDEF}} = 2a.\left( {4 - {a^2}} \right) = 8a - 2{a^3}\).
Để chi phí phần trang trí là nhỏ nhất thì diện tích phần tô màu phải nhỏ nhất hay diện tích hình chữ nhật \(CDEF\) phải lớn nhất.
Xét hàm số \(f\left( a \right) = 8a - 2{a^3}\). Có \(f'\left( a \right) = 8 - 6{a^2} = 0 \Leftrightarrow a = \frac{{2\sqrt 3 }}{3}\) vì \(0 < a < 2\).
Bảng biến thiên
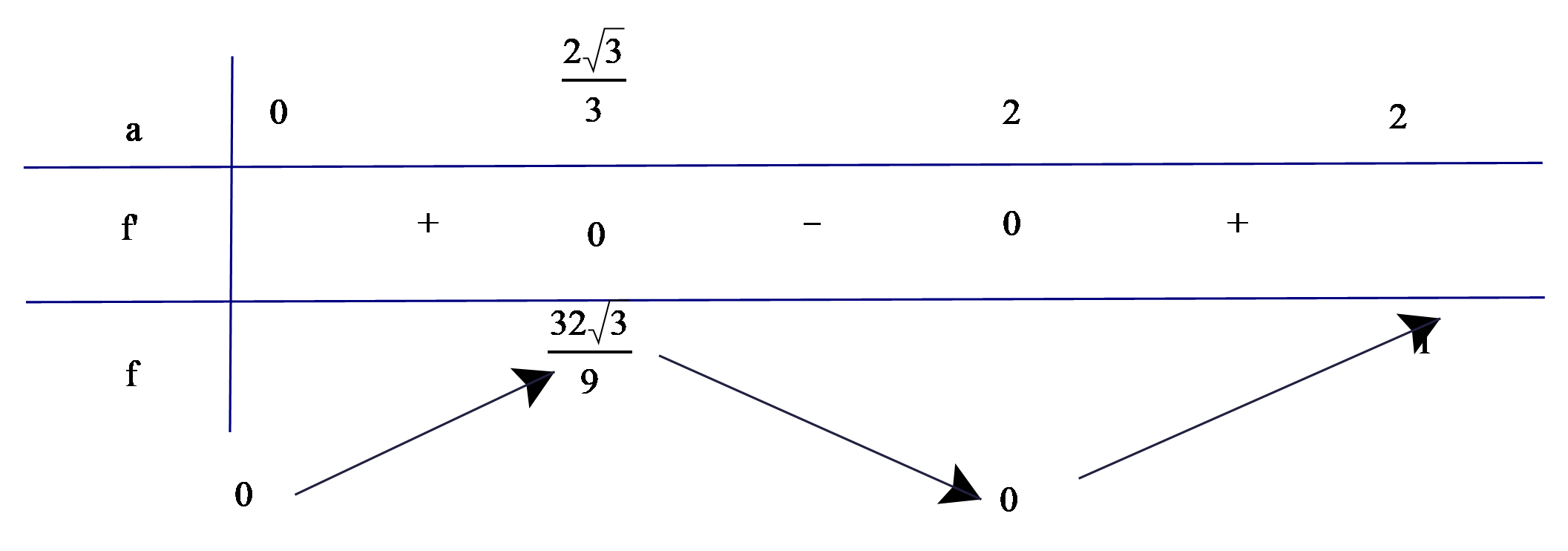
Từ bảng biến thiên ta có diện tích \(CDEF\) lớn nhất bằng \(\frac{{32\sqrt 3 }}{9}\) khi \(a = \frac{{2\sqrt 3 }}{3}\).
Khi đó diện tích phần tô màu là \({S_1} = S - {S_{CDEF}} = \frac{{32}}{3} - \frac{{32\sqrt 3 }}{9}\).
Chi phí tối thiểu là: \(\left( {\frac{{32}}{3} - \frac{{32\sqrt 3 }}{9}} \right).1000000 \approx 4,5\) triệu đồng.
Lời giải
Trả lời: 1309
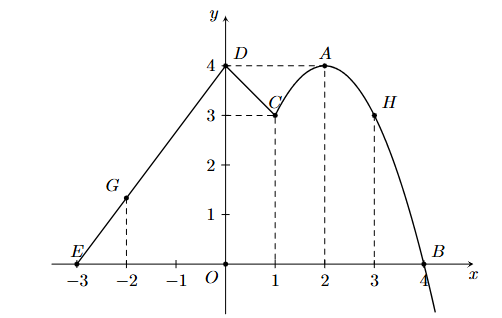
Vì hàm số bậc hai \(f\left( x \right) = a{x^2} + bx + c\left( {a \ne 0} \right)\) có đồ thị là một parabol (P) có đỉnh \(S\left( {1; - 2} \right)\) và cắt trục tung tại điểm có tung độ bằng 1 nên ta có
.Suy ra
Có \(F\left( x \right) = \int {\left( {3{x^2} - 6x + 1} \right)dx} = {x^3} - 3{x^2} + x + C\).
Mà \(F\left( 0 \right) = 1\) nên \(C = 1\). Do đó \(F\left( x \right) = {x^3} - 3{x^2} + x + 1\).
Đồ thị hàm số \(y = F\left( x \right)\) đi qua điểm \(M\left( {12;m} \right)\) nên \({12^3} - {3.12^2} + 12 + 1 = m \Leftrightarrow m = 1309\).
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.