Gọi \({x_1},\;{x_2},\;{x_3},\;{x_4}\)là các nghiệm của phương trình \(\left( {x + 1} \right)\left( {x + 3} \right)\left( {x + 5} \right)\left( {x + 7} \right) = 1\). Tính giá trị của biểu thức \(P = {x_1}.{x_2}.{x_3}.{x_4}\)
Câu 2 (2 điểm) 1) Cho đa thức \[f(x)\] thỏa mãn \[2f\left( x \right) + 3f\left( {2 - x} \right) = 5{x^2} - 8x + 3,\,\,\left( 1 \right)\]với mọi số thực \[x\].
a) Trong đẳng thức \(\left( 1 \right)\), thay \(x\) bởi \(2 - x\) và ghi ra kết quả.
b) Giải phương trình \(f\left( x \right) = - 1\)
Gọi \({x_1},\;{x_2},\;{x_3},\;{x_4}\)là các nghiệm của phương trình \(\left( {x + 1} \right)\left( {x + 3} \right)\left( {x + 5} \right)\left( {x + 7} \right) = 1\). Tính giá trị của biểu thức \(P = {x_1}.{x_2}.{x_3}.{x_4}\)
Câu 2 (2 điểm) 1) Cho đa thức \[f(x)\] thỏa mãn \[2f\left( x \right) + 3f\left( {2 - x} \right) = 5{x^2} - 8x + 3,\,\,\left( 1 \right)\]với mọi số thực \[x\].
a) Trong đẳng thức \(\left( 1 \right)\), thay \(x\) bởi \(2 - x\) và ghi ra kết quả.
b) Giải phương trình \(f\left( x \right) = - 1\)
Quảng cáo
Trả lời:
|
Biến đổi phương trình thành: \(({x^2} + 8x + 11 - 4)({x^2} + 8x + 11 + 4) = 1\) . Đặt \(t = {x^2} + 8x + 11\) và giải được \(t = \sqrt {17} ,\;t = - \sqrt {17} \) . |
|
Với \(t = \sqrt {17} \Rightarrow {x^2} + 8x + 11 - \sqrt {17} = 0\) có \({x_1}.{x_2} = 11 - \sqrt {17} \) |
|
Với \(t = - \sqrt {17} \Rightarrow {x^2} + 8x + 11 + \sqrt {17} = 0\) có \({x_3}.{x_4} = 11 + \sqrt {17} \) |
|
Vậy \(P = {x_1}.{x_2}.{x_3}.{x_4} = (11 - \sqrt {17} )(11 + \sqrt {17} ) = 104\) |
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Lời giải
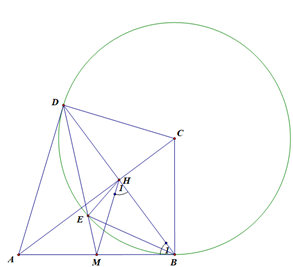
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.