Đề thi tuyển sinh vào lớp 10 môn Toán năm 2023-2024 Chuyên Đắk Lắk có đáp án
32 người thi tuần này 4.6 75 lượt thi 6 câu hỏi 45 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề KSCL THCS Văn Quán - HN_năm học 2025-2026_Tháng 12 có đáp án
Đề KSCL THCS Phú Diễn - HN_năm học 2025-2026_Tháng 12 có đáp án
Đề KSCL THCS Lê Lợi - HN_năm học 2025-2026_Tháng 12 có đáp án
Đề KSCL THCS Thịnh Quang - HN_năm học 2025-2026_Tháng 9 có đáp án
Đề thi tuyển sinh vào lớp 10 môn Toán Sở GD&ĐT Đắk Nông năm học 2025-2026 có đáp án
Đề thi tuyển sinh vào lớp 10 môn Toán Sở GD&ĐT Bắc Kạn năm học 2025-2026 có đáp án
Đề thi tuyển sinh vào lớp 10 môn Toán Sở GD&ĐT Đắk Lắk năm học 2025-2026 có đáp án
Đề thi tuyển sinh vào lớp 10 môn Toán Sở GD&ĐT Long An năm học 2025-2026 có đáp án
Danh sách câu hỏi:
Lời giải
Lời giải
|
Biến đổi phương trình thành: \(({x^2} + 8x + 11 - 4)({x^2} + 8x + 11 + 4) = 1\) . Đặt \(t = {x^2} + 8x + 11\) và giải được \(t = \sqrt {17} ,\;t = - \sqrt {17} \) . |
|
Với \(t = \sqrt {17} \Rightarrow {x^2} + 8x + 11 - \sqrt {17} = 0\) có \({x_1}.{x_2} = 11 - \sqrt {17} \) |
|
Với \(t = - \sqrt {17} \Rightarrow {x^2} + 8x + 11 + \sqrt {17} = 0\) có \({x_3}.{x_4} = 11 + \sqrt {17} \) |
|
Vậy \(P = {x_1}.{x_2}.{x_3}.{x_4} = (11 - \sqrt {17} )(11 + \sqrt {17} ) = 104\) |
Lời giải
Lời giải
|
Gọi \(x,\,x + 1,\,x + 2,\,x + 3,\,x + 4,\,x + 5,\,x + 6,\,x + 7,\,x + 8\) với \(x\) là số nguyên dương lần lượt là cạnh của các hình vuông đã cho, suy ra \[S = {x^2} + {\left( {\,x + 1} \right)^2} + {\left( {\,x + 2} \right)^2} + {\left( {\,x + 3} \right)^2} + {\left( {\,x + 4} \right)^2} + {\left( {\,x + 5} \right)^2} + \,{\left( {x + 6} \right)^2} + {\left( {x + 7} \right)^2} + {\left( {\,x + 8} \right)^2}\] |
|
Rút gọn \[S = 9{x^2} + 72x + 204\]. Gọi hình vuông cần tìm có cạnh là \(y\) với \(y\) là số nguyên dương, ta có \[9{x^2} + 72x + 204 = {y^2}\left( 1 \right)\] |
|
Ta có \[9{x^2} + 72x + 204 = 9\left( {{x^2} + 8x + 22} \right) + 6\] chia cho 9 dư 6. Mặt khác \({y^2}\) chia cho 9 có số dư là \(r \in \left\{ {0;\,1;4;7} \right\}\) suy ra phương trình \(\left( 1 \right)\) vô nghiệm. |
|
Vậy không tồn tại hình vuông thỏa mãn yêu cầu bài toán. |
|
2) Gọi các số tự nhiên \({a_1},{a_2},...,{a_{17}}\) lần lượt là độ dài đường kính 17 đường tròn đã vẽ và \({r_1},{r_2},...,{r_{17}}\) là số dư khi chia lần lượt \({a_1},{a_2},...,{a_{17}}\) cho 5. |
|
Ta có: \({r_1},{r_2},...,{r_{17}} \in {\rm{\{ }}0;1;2;3;4\} \) |
|
Nếu trong 17 số \({r_1},{r_2},...,{r_{17}}\) tồn tại năm số bằng nhau, chẳng hạn: \({r_1} = {r_2} = {r_3} = {r_4} = {r_5}\) Thì ta có \({a_1} + {a_2} + {a_3} + {a_4} + {a_5}\) chia hết cho 5. |
|
Nếu trong 17 số \({r_1},{r_2},...,{r_{17}}\) không có năm số nào bằng nhau, tức là tối đa 4 số bằng nhau, chẳng hạn có 4 nhóm 4 số bằng nhau, như vậy 17 số dư được phân thành 4 lớp mà mỗi lớp có 4 phần tử và 1 lớp có 1 phần tử với các phần tử đại diện là 0;1;2;3;4. Lúc đó lấy trong mỗi lớp 1 số sẽ được năm số có giá trị đôi một khác nhau. Chẳng hạn \({r_1} \ne {r_2} \ne {r_3} \ne {r_4} \ne {r_5}\)và \({r_1} + {r_2} + {r_3} + {r_4} + {r_5} = 10\) nên \({a_1} + {a_2} + {a_3} + {a_4} + {a_5}\) chia hết cho 5. |
Lời giải
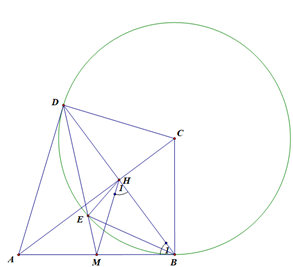
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.