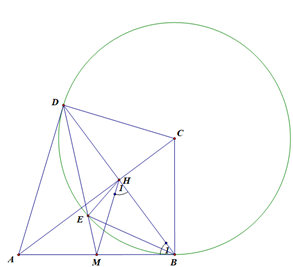
Cho tứ giác \(ABCD\) có \(\widehat {ABC} = \widehat {ADC} = 90^\circ ,\,BC = CD\), \(M\) là trung điểm của \(AB\), đường tròn tâm \(C\) bán kính \(BC\) cắt \(MD\) tại \(E\left( {E \ne D} \right)\), \(H\) là giao điểm của \(AC\) và \(BD\).

1) Chứng minh rằng tứ giác \(BHEM\) là tứ giác nội tiếp.

2) Gọi \(F\) là giao điểm của \(AE\) và đường tròn \(\left( C \right)\,\left( {F \ne E} \right)\). Chứng minh \(BC \bot DF\)

3) Gọi \(I\) là giao điểm của đường thẳng \(BC\) và đường tròn \(\left( C \right)\,\left( {I \ne B} \right)\), \(J\) là giao điểm của \(AI\) và \(DF\). Tính tỉ số \(\frac{{DJ}}{{DF}}\)

a)     Trong đẳng thức \(\left( 1 \right)\), thay \(x\) bởi \(2 - x\) và ghi ra kết quả.

Từ \(\left( 1 \right)\), thay \(x\) bởi \(2 - x\), ta được : \[2f\left( {2 - x} \right) + 3f\left( x \right) = 5{\left( {2 - x} \right)^2} - 8\left( {2 - x} \right) + 3\]\[ \Leftrightarrow 2f\left( {2 - x} \right) + 3f\left( x \right) = 5{x^2} - 12x + 7\]

b)     Giải phương trình \(f\left( x \right) =  - 1\)

Ta có \[\left\{ \begin{array}{l}2f\left( x \right) + 3f\left( {2 - x} \right) = 5{x^2} - 8x + 3\\2f\left( {2 - x} \right) + 3f\left( x \right) = 5{x^2} - 12x + 7\end{array} \right.\].

Giải hệ ta tìm được \(f\left( x \right) = {x^2} - 4x + 3\).

Khi đó \(f\left( x \right) =  - 1 \Leftrightarrow {x^2} - 4x + 3 =  - 1 \Leftrightarrow {\left( {x - 2} \right)^2} = 0 \Leftrightarrow x = 2\)

Giải hệ phương trình sau \(\left\{ \begin{array}{l}{x^3} - 6{x^2} + 13x - 10 - \left( {x - y + 2} \right)\sqrt {x - y + 1}  = 0\\\left( {3{x^2} + 18x - 2xy + 6y - {y^2}} \right)\sqrt {x - y + 6}  - 24x - 8y = 0.\end{array} \right.\)

Xét phương trình \({x^3} - 6{x^2} + 13x - 10 - \left( {x - y + 2} \right)\sqrt {x - y + 1}  = 0\left( 1 \right)\)

Điều kiện: \(x - y + 1 \ge 0\).

\[\left( 1 \right) \Leftrightarrow \left( {{x^3} - 6{x^2} + 12x - 8} \right) + \left( {x - 2} \right) = \sqrt {x - y + 1} \left( {x - y + 1} \right) + \sqrt {x - y + 1} \]

\( \Leftrightarrow {\left( {x - 2} \right)^3} + \left( {x - 2} \right) = {\left( {\sqrt {x - y + 1} } \right)^3} + \sqrt {x - y + 1} \left( 2 \right)\).

Đặt \(\left\{ \begin{array}{l}u = x - 2\\v = \sqrt {x - y + 1} \end{array} \right.\), khi đó \(\left( 2 \right) \Leftrightarrow {u^3} + u = {v^3} + v\) \( \Leftrightarrow \left( {u - v} \right)\left( {{u^2} + {v^2} + uv + 1} \right) = 0 \Leftrightarrow u = v\)\( \Leftrightarrow \sqrt {x - y + 1}  = x - 2\)

Xét phương trình \(\left( {3{x^2} + 18x - 2xy + 6y - {y^2}} \right)\sqrt {x - y + 6}  - 24x - 8y = 0\)

\( \Leftrightarrow \left( {3{x^2} - 2xy - {y^2} + 18x + 6y} \right)\sqrt {x - y + 6}  - 24x - 8y = 0\)

\( \Leftrightarrow \left[ {\left( {3{x^2} - 2xy - {y^2}} \right) + 6\left( {3x + y} \right)} \right]\sqrt {x - y + 6}  - 8\left( {3x + y} \right) = 0\)

\( \Leftrightarrow \left[ {\left( {3x + y} \right)\left( {x - y} \right) + 6\left( {3x + y} \right)} \right]\sqrt {x - y + 6}  - 8\left( {3x + y} \right) = 0\)

\( \Leftrightarrow \left( {3x + y} \right)\left[ {{{\left( {\sqrt {x - y + 6} } \right)}^3} - 8} \right] = 0 \Leftrightarrow 3x + y = 0\) (do \(x - y + 1 \ge 0 \Rightarrow {\left( {\sqrt {x + y + 6} } \right)^3} - 8 > 0\))

Ta có hệ phương trình \(\left\{ \begin{array}{l}3x =  - y\\\sqrt {x - y + 1}  = x - 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}3x =  - y\\\sqrt {4x + 1}  = x - 2\end{array} \right.\)

\( \Leftrightarrow \left\{ \begin{array}{l}3x =  - y\\x \ge 2\\{x^2} - 8x + 3 = 0\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}3x =  - y\\\left[ \begin{array}{l}x = 4 + \sqrt {13} \\x = 4 - \sqrt {13} \end{array} \right.\\x \ge 2\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}x = 4 + \sqrt {13} \\y =  - 12 - 3\sqrt {13} \end{array} \right.\)