Trong tháng 4 năm 2023, hai hộ gia đình bác An và bác Bình dùng hết tổng cộng 500 nghìn đồng tiền điện. Sang tháng 5 năm 2023, do tăng cường thực hiện việc sử dụng điện an toàn, tiết kiệm và hiệu quả; nhà bác An giảm được 15% tiền điện và nhà bác Bình giảm được 10% tiền điện; kết quả là cả hai hộ gia đình tiết kiệm được tổng cộng 65 nghìn đồng tiền điện so với tháng 4 năm 2023. Hỏi trong tháng 4 năm 2023, mỗi hộ gia đình dùng hết bao nhiêu đồng tiền điện?
Trong tháng 4 năm 2023, hai hộ gia đình bác An và bác Bình dùng hết tổng cộng 500 nghìn đồng tiền điện. Sang tháng 5 năm 2023, do tăng cường thực hiện việc sử dụng điện an toàn, tiết kiệm và hiệu quả; nhà bác An giảm được 15% tiền điện và nhà bác Bình giảm được 10% tiền điện; kết quả là cả hai hộ gia đình tiết kiệm được tổng cộng 65 nghìn đồng tiền điện so với tháng 4 năm 2023. Hỏi trong tháng 4 năm 2023, mỗi hộ gia đình dùng hết bao nhiêu đồng tiền điện?
Quảng cáo
Trả lời:
Gọi số tiền điện trong tháng 4 của nhà bác An là \(x\) (nghìn đồng), đkiện \(0 < x < 500\)
Gọi số tiền điện trong tháng 4 của nhà bác Bình là \(y\) (nghìn đồng), đkiện \(0 < y < 500\)Vì trong tháng 4 cả hai gia đình dùng hết 500 nghìn tiền điện nên ta có phương trình
\(x + y = 500\) (1)Vì sang tháng 5 nhà bác An giảm \(15\% \) và nhà bác Bình giảm \(10\% \) và cả hai nhà giảm được 65 nghìn đồng nên ta có phương trình
\(15\% x + 10\% y = 65 \Leftrightarrow 0,15x + 0,1y = 65\) (2)Từ (1) và (2) ta có hệ phương trình:\(\left\{ \begin{array}{l}x + y = 500\\0,15x + 0,1y = 65\end{array} \right.\)
Giải hệ ta được \(\left\{ \begin{array}{l}x = 300\\y = 200\end{array} \right.\). Vậy trong tháng 4 nhà bác An dùng hết 300 nghìn đồng tiền điện, nhà bác Bình dùng hết 200 nghìn đồng tiền điện.Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Có \(a + b + c = 1\)\( \Rightarrow c = c\left( {a + b + c} \right) \Rightarrow c + ab = c\left( {a + b + c} \right) + ab = \left( {c + a} \right)\left( {c + b} \right)\)
Áp dụng BĐT AM - GM với hai số dương \(x,\,\,y\) ta có: .
Dấu “=” xảy ra khi \(x = y\)
\( \Rightarrow \frac{1}{{\sqrt {c + ab} }} = \frac{1}{{\sqrt {\left( {c + a} \right)\left( {c + b} \right)} }} \le \frac{{\frac{1}{{c + a}} + \frac{1}{{c + b}}}}{2}\, \Rightarrow \frac{{ab}}{{\sqrt {c + ab} }} \le \frac{{ab}}{2}\left( {\frac{1}{{c + a}} + \frac{1}{{c + b}}} \right)\,\,\left( 1 \right)\)Tương tự:
\(\frac{{bc}}{{\sqrt {a + bc} }} \le \frac{{bc}}{2}\left( {\frac{1}{{b + c}} + \frac{1}{{b + a}}} \right)\,\,\left( 2 \right)\) \(\frac{{ca}}{{\sqrt {b + ca} }} \le \frac{{ca}}{2}\left( {\frac{1}{{b + c}} + \frac{1}{{b + a}}} \right)\,\,\left( 3 \right)\)
Cộng (1), (2), (3) theo vế ta có:
\(P = \frac{{ab}}{{\sqrt {c + ab} }} + \frac{{bc}}{{\sqrt {a + bc} }} + \frac{{ca}}{{\sqrt {b + ca} }}\)
Từ đó giá trị lớn nhất của \(P\) là đạt được khi và chỉ khi \(a = b = c = \frac{1}{3}\).Lời giải
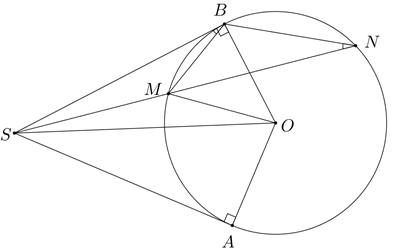 \(\widehat {SAO} = 90^\circ \) vì \(SA\) là tiếp tuyến của đường tròn |
|
|
\(\widehat {SBO} = 90^\circ \) vì \(SB\) là tiếp tuyến của đường tròn |
|
|
\( \Rightarrow \widehat {SAO} + \widehat {SBO} = 180^\circ \) |
|
|
Vậy tứ giác \(SAOB\) nội tiếp. |
|
|
2. Chứng minh \(S{B^2} = SM.\,\,SN\). |
|
|
Xét hai \[\Delta SBM\] và\[\Delta SNB:\]Có \(\widehat S\) chung. |
|
|
Có \(\widehat {MBS} = \widehat {MNB}\) (cùng chắn )\[ \Rightarrow \Delta SBM\] đồng dạng \[\Delta SNB\] |
|
|
\( \Rightarrow \frac{{SB}}{{SN}} = \frac{{SM}}{{SB}} \Leftrightarrow S{B^2} = SM.\,\,SN\) |
|
|
3. Cho \(SO = R\sqrt 5 \)và \(MN = R\sqrt 2 \). Gọi \(E\) là trung điểm \(MN\). Tính độ dài đoạn thẳng \(OE\) và diện tích tam giác \(SOM\) theo \(R\). |
|
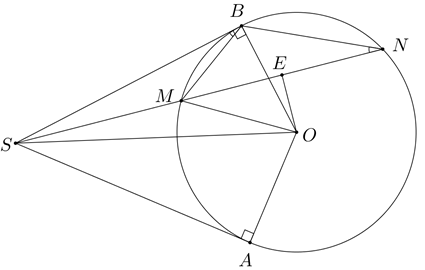 Ta có \(OE \bot MN\) \(MN = R\sqrt 2 \Rightarrow ME = \frac{{R\sqrt 2 }}{2},\) \(OM = R\) \( \Rightarrow OE = \sqrt {O{M^2} - M{E^2}} = \frac{{R\sqrt 2 }}{2}\) |
|
|
\(SO = R\sqrt 5 ,\)\(SE = \sqrt {S{O^2} - O{E^2}} = \sqrt {5{R^2} - \frac{{2{R^2}}}{4}} = \frac{{3R\sqrt 2 }}{2}\) |
|
|
\(SM = SE - ME = R\sqrt 2 .\) |
|
|
Vậy \({S_{SOM}} = \frac{1}{2}OE.SM = \frac{1}{2}.\frac{{R\sqrt 2 }}{2}.R\sqrt 2 = \frac{{{R^2}}}{2}\) |
|
|
4. Tiếp tuyến tại \(M\) của đường tròn \(\left( {O;R} \right)\) cắt \(SA,\,SB\) lần lượt tại \(P,\,Q\). Gọi giao điểm của \(OQ,\,OP\) với \(AB\) lần lượt là \(I\) và \(H\). Chứng minh ba đường thẳng \(OM,\,\,QH,\,\,PI\) đồng quy. |
|
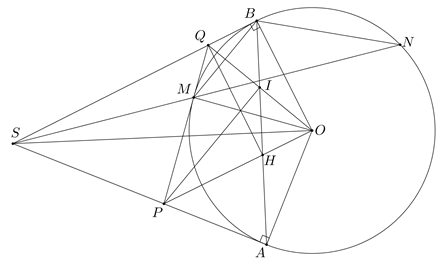 Vì \(QM,\,\,QB\) là hai tiếp tuyến của nên là hai tiếp tuyến của nên
|
|
|
|
|
|
Ta có \(OM \bot PQ\,\,\,\left( 3 \right)\) Từ (1), (2) và (3) suy ra ba đường thẳng \(OM,\,\,QH,\,\,PI\) là ba đường cao của tam giác \(OPQ\) nên chúng đồng quy. |
|
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.