(3,5 điểm)
1. Giải các phương trình, bất phương trình sau:
a) \[\frac{x}{{x + 3}} - \frac{2}{{x - 3}} = \frac{{ - 2x - 6}}{{{x^2} - 9}}\].
(3,5 điểm)
1. Giải các phương trình, bất phương trình sau:
a) \[\frac{x}{{x + 3}} - \frac{2}{{x - 3}} = \frac{{ - 2x - 6}}{{{x^2} - 9}}\].Quảng cáo
Trả lời:
a) \[\frac{x}{{x + 3}} - \frac{2}{{x - 3}} = \frac{{ - 2x - 6}}{{{x^2} - 9}}\]
\[\frac{{x\left( {x - 3} \right)}}{{\left( {x + 3} \right)\left( {x - 3} \right)}} - \frac{{2\left( {x + 3} \right)}}{{\left( {x + 3} \right)\left( {x - 3} \right)}} = \frac{{ - 2x - 6}}{{\left( {x + 3} \right)\left( {x - 3} \right)}}\]
\[x\left( {x - 3} \right) - 2\left( {x + 3} \right) = - 2x - 6\]
\[{x^2} - 5x - 6 = - 2x - 6\]
\[{x^2} - 3x = 0\]
\(x\left( {x - 3} \right) = 0\)
\(x = 0\) hoặc \(x - 3 = 0\)
\(x = 0\) (thỏa mãn) hoặc \(x = 3\) (không thỏa mãn).
Vậy phương trình đã cho có nghiệm là \(x = 0.\)Câu hỏi cùng đoạn
Câu 2:
1. Giải các phương trình, bất phương trình sau:
b)
\[\left( {{x^2} - {x^2}} \right) + \left( {4x - x} \right) < - 4 - 3\]
\[3x < - 7\]
\[x < - \frac{7}{3}\].
Vậy nghiệm của bất phương trình là \[x < - \frac{7}{3}.\]
Câu 3:
1. Giải các phương trình, bất phương trình sau:
c) \(\sqrt {9x - 9} - \sqrt {4x - 4} + \sqrt {x - 1} = 16.\)
c) \(\sqrt {9x - 9} - \sqrt {4x - 4} + \sqrt {x - 1} = 16\) (ĐKXĐ: \(x \ge 1)\)
\(\sqrt {9\left( {x - 1} \right)} - \sqrt {4\left( {x - 1} \right)} + \sqrt {x - 1} = 16\)
\(3\sqrt {x - 1} - 2\sqrt {x - 1} + \sqrt {x - 1} = 16\)
\(2\sqrt {x - 1} = 16\)
\(\sqrt {x - 1} = 8\)
\(x - 1 = 16\)
\(x = 17\) (thỏa mãn).
Vậy phương trình đã cho có nghiệm \(x = 17.\)
Câu 4:
Giải bài toán sau bằng cách lập hệ phương trình:
Sĩ số lớp 9A là 47 học sinh; trong đó có 35 học sinh nam và 12 học sinh nữ. Nhân dịp sinh nhật của bạn Bình là một thành viên trong lớp; để chuẩn bị các món quà cho Bình, giáo viên chủ nhiệm lớp 9A đã giao nhiệm vụ đến các thành viên còn lại trong lớp như sau:
− Mỗi học sinh nam sẽ làm một bao thư và trang trí.
− Mỗi học sinh nữ sẽ chuẩn bị 3 hoặc 5 tấm thiệp và ghi những lời chúc ý nghĩa gửi đến Bình.

Đến ngày sinh nhật của Bình; Bình đã nhận được rất nhiều tấm thiệp chúc mừng sinh nhật được chứa trong các bao thư rất đẹp.
Hỏi Bình là nam hay nữ? Tính số học sinh nữ làm 5 tấm thiệp. Biết rằng mỗi bao thư chỉ chứa 1 tấm thiệp bên trong và Bình không tham gia nhiệm vụ của giáo viên chủ nhiệm.
Giải bài toán sau bằng cách lập hệ phương trình:
|
Sĩ số lớp 9A là 47 học sinh; trong đó có 35 học sinh nam và 12 học sinh nữ. Nhân dịp sinh nhật của bạn Bình là một thành viên trong lớp; để chuẩn bị các món quà cho Bình, giáo viên chủ nhiệm lớp 9A đã giao nhiệm vụ đến các thành viên còn lại trong lớp như sau: − Mỗi học sinh nam sẽ làm một bao thư và trang trí. − Mỗi học sinh nữ sẽ chuẩn bị 3 hoặc 5 tấm thiệp và ghi những lời chúc ý nghĩa gửi đến Bình. |
|
Đến ngày sinh nhật của Bình; Bình đã nhận được rất nhiều tấm thiệp chúc mừng sinh nhật được chứa trong các bao thư rất đẹp.
Hỏi Bình là nam hay nữ? Tính số học sinh nữ làm 5 tấm thiệp. Biết rằng mỗi bao thư chỉ chứa 1 tấm thiệp bên trong và Bình không tham gia nhiệm vụ của giáo viên chủ nhiệm.
2. Gọi \[x\] (học sinh) là số học sinh nữ làm 3 tấm thiệp
\[y\] (học sinh) là số học sinh nữ làm 5 tấm thiệp \(\left( {x,\,\,y \in \mathbb{N}*} \right)\)
⦁ Giả sử Bình là nam
Số nam tham gia nghiệm vụ là 34 học sinh; số nữ tham gia nhiệm vụ là 12 học sinh.
Ta có hệ phương trình: \(\left\{ \begin{array}{l}x + y = 12\\3x + 5y = 34\end{array} \right.\) (I)
Giải hệ phương trình (I) ta được \(\left\{ \begin{array}{l}x = 13\\y = - 1\end{array} \right.\) (loại)
Có thể kết luận bằng phương pháp loại suy.
⦁ Giả sử Bình là nữ
Số nam tham gia nghiệm vụ là 35 học sinh, số nữ tham gia nhiệm vụ là 11 học sinh.
Ta có hệ phương trình: \(\left\{ \begin{array}{l}x + y = 11\\3x + 5y = 35\end{array} \right.\) (II)
Giải hệ phương trình (II) ta được \(\left\{ \begin{array}{l}x = 10\\y = 1\end{array} \right.\) (TM)
Vậy Bình là nữ và có 1 học sinh nữ làm 5 tấm thiệp.
Câu 5:
3. Trong một cuộc thi tuyển dụng việc làm, ban tổ chức quy định mỗi người ứng tuyển phải trả lời 25 câu hỏi ở vòng sơ tuyển. Mỗi câu hỏi này có sẵn bốn đáp án, trong đó chỉ có một đáp án chung. Người ứng tuyển chọn đáp án đúng sẽ được cộng 2 điểm, chọn đáp án sai bị trừ 1 điểm. Ở vòng sơ tuyển, ban tổ chức tặng cho mỗi người dự thi 5 điểm và theo quy định ứng tuyển phải trả lời hết 25 câu hỏi; người nào có số điểm từ 25 điểm trở lên mới được dự thi vòng tiếp theo.
a) Hãy viết một bất phương trình mô tả tình huống này.
b) Hỏi người ứng tuyển phải trả lời chính xác ít nhất bao nhiêu câu hỏi ở vòng sơ tuyển mới được vào vòng tiếp theo?
3. Trong một cuộc thi tuyển dụng việc làm, ban tổ chức quy định mỗi người ứng tuyển phải trả lời 25 câu hỏi ở vòng sơ tuyển. Mỗi câu hỏi này có sẵn bốn đáp án, trong đó chỉ có một đáp án chung. Người ứng tuyển chọn đáp án đúng sẽ được cộng 2 điểm, chọn đáp án sai bị trừ 1 điểm. Ở vòng sơ tuyển, ban tổ chức tặng cho mỗi người dự thi 5 điểm và theo quy định ứng tuyển phải trả lời hết 25 câu hỏi; người nào có số điểm từ 25 điểm trở lên mới được dự thi vòng tiếp theo.
a) Hãy viết một bất phương trình mô tả tình huống này.
b) Hỏi người ứng tuyển phải trả lời chính xác ít nhất bao nhiêu câu hỏi ở vòng sơ tuyển mới được vào vòng tiếp theo?
3. a) Gọi \(x\) là số câu trả lời đúng \(\left( {0 \le x \le 25\,,\,\,x \in \mathbb{N}*} \right).\)
Số câu trả lời sau là \(25 - x\) (câu).
Trả lời đúng \(x\) câu hỏi được cộng \(2x\) (điểm)
Trả lời sai \(25 - x\) câu hỏi bị trừ \(25 - x\) (điểm)
\(3x - 25 \ge 25\)Vì vậy, sau khi trả lời 25 câu thì người dự thi sẽ có số điểm là:
\(2x - \left( {25 - x} \right) = 2x - 25 + x = 3x - 25\) (điểm).
Theo bài, để được dự thi tiếp vòng sau thì có số điểm từ 25 trở lên, nên ta có bất phương trình
\(3x - 25 \ge 25\).
Vậy bất phương trình cần tìm là \(3x - 25 \ge 25\).
b) Giải bất phương trình \(3x - 25 \ge 25\), ta được:
\(3x \ge 50\)
\(x \ge \frac{{50}}{3}\,\,\,( \approx 16,7)\).
Mà \(0 \le x \le 25\,,\,\,x \in \mathbb{N}*\) nên người ứng tuyển cần phải trả lời chính xác ít nhất thì mới được dự thi tiếp vòng sau.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Hướng dẫn giải
a) – Xét biểu thức \(A = \frac{{\sqrt x + 2}}{{\sqrt x - 4}}\).
Điều kiện xác định của biểu thức \(A\) và \(x \ge 0\) và \(\sqrt x - 4 \ne 0\) hay \(x \ge 0,\,\,x \ne 16.\)
– Xét biểu thức \[B = \frac{{\sqrt x - 2}}{{\sqrt x + 4}} - \frac{{10\sqrt x - 8}}{{16 - x}}\].
Với \(x \ge 0\), ta có:
⦁ \[16 - x = \left( {4 + \sqrt x } \right)\left( {4 - \sqrt x } \right) = - \left( {\sqrt x + 4} \right)\left( {\sqrt x - 4} \right)\].
⦁ \(x \ge 0\) nên \(\sqrt x \ge 0,\) suy ra \(\sqrt x + 4 > 0.\)
Điều kiện xác định của biểu thức \(B\) là \(x \ge 0\) và \(\sqrt x - 4 \ne 0\) hay \(x \ge 0,\,\,x \ne 16.\)
Vậy điều kiện xác định của biểu thức \(A\) và biểu thức \(B\) đều là \(x \ge 0,\,\,x \ne 16.\)
Lời giải
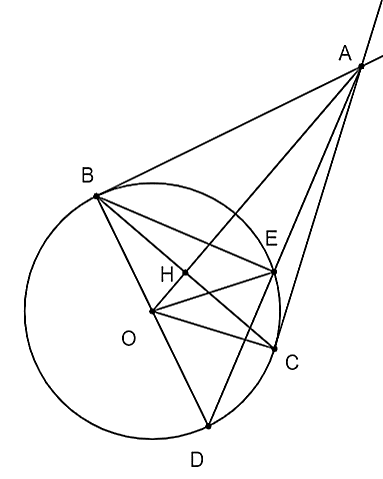
a) Xét đường tròn \[\left( O \right)\] có: \[AB,AC\] lần lượt là tiếp tuyến tại \[B,C\] nên \[AB = AC\] (tính chất hai tiếp tuyến cắt nhau) .
Suy ra \[A\] thuộc đường trung trực của \[BC\].
Mà \[OB = OC = R\] nên \[O\] thuộc đường trung trực của \[BC\]
Do đó \[OA\] là đường trung trực của \[BC\] nên \[OA \bot BC\] tại \[H\].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.