Cho tam giác ABC nhọn, không cân, nội tiếp đường tròn (O). Gọi E là điểm đối xứng của B qua AC và F điểm đối xứng của C qua AB. Đường thẳng BE cắt đường thẳng CF tại H.
a) Chứng minh các tứ giác AHBF và AHCE là tứ giác nội tiếp.
b) Đường tròn ngoại tiếp các tam giác ABE và ACF cắt nhau tại điểm thứ hai là D. Chứng minh F,B,D thẳng hàng và DA là tia phân giác của góc EDF.
c) Gọi P, Q lần lượt là tâm đường tròn ngoại tiếp các tam giác ABE, ACF. Chứng minh sáu điểm B, C, D, O, P, Q cùng thuộc một đường tròn tâm I và giao điểm (khác D) của đường thẳng AD với đường tròn (I) là trực tâm tam giác APQ.
d) Giả sử H thuộc đường tròn (I). Chứng minh các đường thẳng AI, DH, BC, PQ đồng quy.
Cho tam giác ABC nhọn, không cân, nội tiếp đường tròn (O). Gọi E là điểm đối xứng của B qua AC và F điểm đối xứng của C qua AB. Đường thẳng BE cắt đường thẳng CF tại H.
a) Chứng minh các tứ giác AHBF và AHCE là tứ giác nội tiếp.
b) Đường tròn ngoại tiếp các tam giác ABE và ACF cắt nhau tại điểm thứ hai là D. Chứng minh F,B,D thẳng hàng và DA là tia phân giác của góc EDF.
c) Gọi P, Q lần lượt là tâm đường tròn ngoại tiếp các tam giác ABE, ACF. Chứng minh sáu điểm B, C, D, O, P, Q cùng thuộc một đường tròn tâm I và giao điểm (khác D) của đường thẳng AD với đường tròn (I) là trực tâm tam giác APQ.
d) Giả sử H thuộc đường tròn (I). Chứng minh các đường thẳng AI, DH, BC, PQ đồng quy.
Quảng cáo
Trả lời:
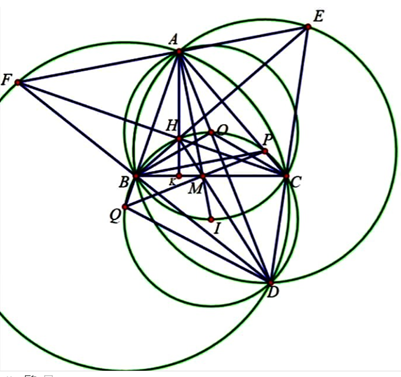
a) AFB=ACB (đối xứng); AHB=KHE (đối đỉnh)
Mà ACB + KHE =180\(^\circ \) nên AHBF nội tiếp.
Tương tự với AHCE.
b) *AED = AHF (cùng bù với AHC) mà AHF = ABF (tứ giác AHBF nội tiếp). Do đó AED = ABF.
Mặt khác AED + ABD = 180\(^\circ \) (ABDE nội tiếp) nên ABF + ABD=180\(^\circ \). Do đó F,B,D thẳng hàng.
Tương tự E,C,D thẳng hàng.
*ADF = ACF, ADE = ABE mà ACF = ABE (cùng phụ với BAC) nên ADF =ADE hay DA là tia phân giác góc EDF.
c) * Dễ thấy P thuộc AC, Q thuộc AB.
* ADC = AFC mà AFC = ACF = 90\(^\circ \)-BAC nên ADC=90o-BAC.
Tương tự ADB = 900-BAC. Vậy BDC = 1800-2BAC.
Lại có BOC = 2BAC (góc nội tiếp và góc ở tâm) nên BDC + BOC = 180o. Suy ra tứ giác BOCD nội tiếp.
* Tam giác PAB cân tại P nên APB = 1800-2BAC. Suy ra PAB = BDC nên tứ giác BPCD nội tiếp.
Tương tự ta có tứ giác BQDC nội tiếp.
* Vậy 6 điểm B, C, D, O, P, Q cùng thuộc một đường tròn (I).
* Dễ CM O thuộc AD. Do đó giao điểm khác D của AD và (I) là O.
* Vì OP là đường trung trực của AB nên OP vuông góc với AB; OQ là đường trung trực của AC nên OQ vuông góc với AC. Vậy O là trực tâm của tam giác APQ.
d) Dễ CM được I là giao điểm của tia phân giác của góc BAC với (O). Gọi M là giao điểm của AI và BC thì HD, PQ đi qua M. Do đó 4 đường AI, BC, HD, PQ đồng quy tại M.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Áp dụng BĐT Cô-si ta có:
\(\sqrt {{b^3} + 1} \) = \(\sqrt {\left( {b + 1} \right)\left( {{b^2} - b + 1} \right)} \) \( \le \) \(\frac{{b + 1 + \;{b^2} - b + 1}}{2} = \) \(\frac{{{b^2} + \;2}}{2}\)
T2: \(\sqrt {{c^3} + 1} \) \( \le \) \(\frac{{{c^2} + \;2}}{2}\) ; \(\sqrt {{a^3} + 1} \) \( \le \) \(\frac{{{a^2} + \;2}}{2}\)
Do đó VT \( \ge \) \(\frac{{2a}}{{{b^2} + \;2}}\) + \(\frac{{2b}}{{{c^2} + \;2}}\) + \(\frac{{2c}}{{{a^2} + \;2}}\)
Ta cần CM: S = \(\frac{{2a}}{{{b^2} + \;2}}\) + \(\frac{{2b}}{{{c^2} + \;2}}\) + \(\frac{{2c}}{{{a^2} + \;2}}\) \( \ge \) 2
Ta có: \(\frac{{2a}}{{{b^2} + \;2}}\) = \(\frac{{a\left( {{b^2} + 2} \right) - a{b^2}}}{{{b^2} + \;2}}\) = a - \(\frac{{a{b^2}}}{{{b^2} + \;2}}\)
Lại có : \(\frac{{a{b^2}}}{{{b^2} + \;2}}\) = \(\frac{{2a{b^2}}}{{{b^2} + {b^2} + \;4}}\) \( \le \) \(\frac{{2a{b^2}}}{{{3^3}\sqrt {{b^4}.\;\;4} }}\) = \(\frac{{{a^3}\sqrt {2{b^2}} }}{3}\) \( \le \) \(\frac{{a.\left( {2 + b + b} \right)}}{9}\) = \(\frac{{2a.\left( {b + 1} \right)}}{9}\)
T2 ta được S \( \ge \) a + b + c - \(\frac{{2.\left( {a + b + c} \right)}}{9}\) - \(\frac{{2\left( {ab + bc + ca} \right)}}{9}\) = \(\frac{{7.\left( {a + b + c} \right)}}{9}\) - \(\frac{{2\left( {ab + bc + ca} \right)}}{9}\)
Ta có ab + bc + ca \( \le \) \(\frac{{{{\left( {a + b + c} \right)}^2}}}{3}\)
Do đó S \( \ge \) \(\frac{{7\;.\;6}}{9}\) - \(\frac{2}{9}\) . \(\frac{{{6^2}}}{9}\) = 2
Dấu bằng xảy ra khi a = b = c = 2. Ta có đpcm.
Lời giải
a) Vì p là SNT lẻ nên p chỉ có 1 trong 2 dạng:
4k + 1 hoặc 4k + 3
Vì (x2 + 1) \( \vdots \;\)p nên p có dạng 4x + 1, hay p – 1 = 4k \( \vdots \) 4.
b) Tồn tại STN x sao cho 2023p + 23p – 24 = x2
\( \Leftrightarrow \) x2 + 1 = 2023p + 23p – 23
Theo Fermat nhỏ, ta có 23p – 23 \( \equiv \) 0 (mod p)
=> 2023p + 23p – 23 \( \equiv \) 0 (mod p)
=> x2 + 1\( \equiv \) 0 (mod p) => p = 4k + 1
=> 2023p + 23p – 24 \( \equiv \;\)-p + (-1)p \( \equiv \) 2 (mod 4)
Mà x2 \( \equiv \) 0,1 (mod 4), mâu thuẫn
Vậy 2023p + 23p – 24 không là số chính phương.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.