Cho p là một số nguyên tố.

a) Chứng minh nếu p lẻ và tồn tại số nguyên x sao cho (x2 + 1) \( \vdots \;\)p thì (p − 1) \( \vdots \) 4.

b) Chứng minh 2023p + 23p – 24 không là số chính phương.

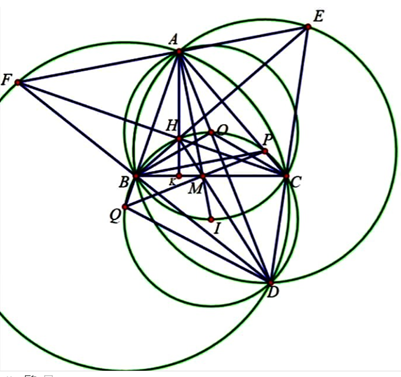
a) AFB=ACB (đối xứng); AHB=KHE (đối đỉnh)

Mà ACB + KHE =180\(^\circ \) nên AHBF nội tiếp.

Tương tự với AHCE.

b) *AED = AHF (cùng bù với AHC) mà AHF = ABF (tứ giác AHBF nội tiếp). Do đó AED = ABF.

Mặt khác AED + ABD = 180\(^\circ \) (ABDE nội tiếp) nên ABF + ABD=180\(^\circ \). Do đó F,B,D thẳng hàng.

Tương tự E,C,D thẳng hàng.

*ADF = ACF, ADE = ABE mà ACF = ABE (cùng phụ với BAC) nên ADF =ADE hay DA là tia phân giác góc EDF.

c) * Dễ thấy P thuộc AC, Q thuộc AB.

* ADC = AFC mà AFC = ACF = 90\(^\circ \)-BAC nên ADC=90o-BAC.

Tương tự ADB = 900-BAC. Vậy BDC = 1800-2BAC.

Lại có BOC = 2BAC (góc nội tiếp và góc ở tâm) nên BDC + BOC = 180o. Suy ra tứ giác BOCD nội tiếp.

* Tam giác PAB cân tại P nên APB = 1800-2BAC. Suy ra PAB = BDC nên tứ giác BPCD nội tiếp.

Tương tự ta có tứ giác BQDC nội tiếp.

* Vậy 6 điểm B, C, D, O, P, Q cùng thuộc một đường tròn (I).

* Dễ CM O thuộc AD. Do đó giao điểm khác D của AD và (I) là O.

* Vì OP là đường trung trực của AB nên OP vuông góc với AB; OQ là đường trung trực của AC nên OQ vuông góc với AC. Vậy O là trực tâm của tam giác APQ.

d) Dễ CM được I là giao điểm của tia phân giác của góc BAC với (O). Gọi M là giao điểm của AI và BC thì HD, PQ đi qua M. Do đó 4 đường AI, BC, HD, PQ đồng quy tại M.

b)Vì a, b, c là 3 nghiệm của f(x) nên ta có

\(\left\{ {\begin{array}{*{20}{c}}{{a^3} - 23a + 24 = 0}\\{{b^3} - 23b + 24 = 0}\\{{c^3} - 23c + 24 = 0}\end{array}} \right.\)  \( \Leftrightarrow \) \(\left\{ {\begin{array}{*{20}{c}}{{a^3} = 23a - 24}\\{{b^3} = 23b - 24}\\{{c^3} = 23c - 24}\end{array}} \right.\) 

\( \Rightarrow \) Q = 23(a + b + c) – 72

Theo Viet:  a + b + c = 0

Do đó   Q = -72