(4,0 điểm)
Một ống đồng hình trụ có chiều cao gấp \[5\] lần bán kính. Biết thể tích ống đồng bằng\(40\pi \,{\rm{c}}{{\rm{m}}^{\rm{3}}}\). Tính chiều cao của ống đồng đó.
Quảng cáo
Trả lời:
Vì ống đồng hình trụ có \(h = 5R\) nên: \[{V_{ongdong}} = {S_d}.h\] \[ = \pi {R^2}h\] \[ = \pi {R^2}5R\] \[ = 5\pi {R^3}\]
\( \Rightarrow {R^3} = \frac{{{V_{ongdong}}}}{{5\pi }}\) \( = \frac{{40\pi }}{{5\pi }}\) \( = 8\)
\( \Rightarrow R = 2\)\( \Rightarrow h = 10\,\,{\rm{(cm)}}\)
Vậy chiều cao của ống đồng là \(10\,\,{\rm{(cm)}}\).
Câu hỏi cùng đoạn
Câu 2:
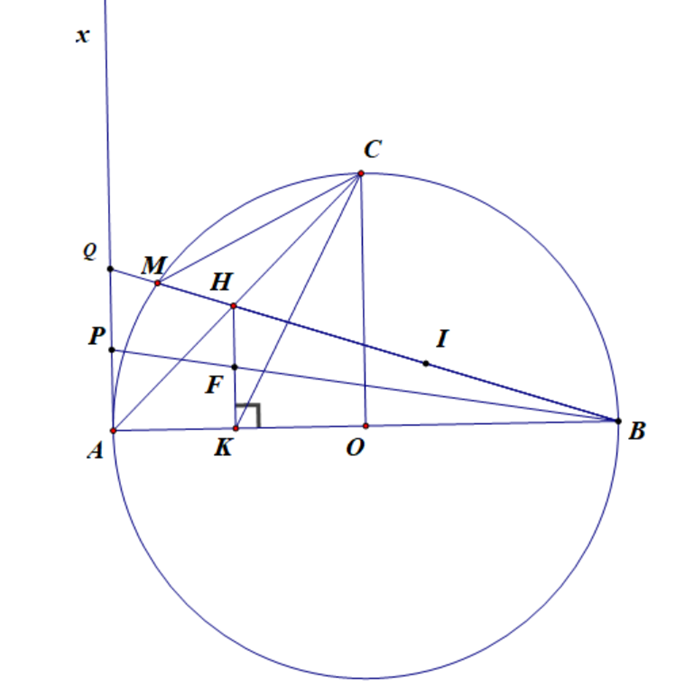
Cho \(\left( {O;R} \right)\) đường kính\[AB\]. Bán kính \[CO\] vuông góc với \[AB\], \[M\]là điểm bất kì trên cung nhỏ \[AC\]( \[M\] khác \[A\] và \[C\]), \[MB\] cắt \[AC\]tại\[H\]. Gọi \[K\] là hình chiếu của \[H\] trên\[AB\].
a) Chứng minh bốn điểm \[C,{\rm{ }}B,{\rm{ }}H,{\rm{ }}K\] cùng thuộc một đường tròn.
b) Chứng minh \[CA\] là phân giác \(\widehat {MCK}\).
c) Kẻ \[Ax\] là tiếp tuyến của nửa đường tròn tại\[A\]. Lấy \(P \in Ax\) sao cho \(\frac{{AP.MB}}{{MA}} = R\).
Chứng minh \[PB\] đi qua trung điểm của đoạn thẳng\[HK\].
Cho \(\left( {O;R} \right)\) đường kính\[AB\]. Bán kính \[CO\] vuông góc với \[AB\], \[M\]là điểm bất kì trên cung nhỏ \[AC\]( \[M\] khác \[A\] và \[C\]), \[MB\] cắt \[AC\]tại\[H\]. Gọi \[K\] là hình chiếu của \[H\] trên\[AB\].
a) Chứng minh bốn điểm \[C,{\rm{ }}B,{\rm{ }}H,{\rm{ }}K\] cùng thuộc một đường tròn.
b) Chứng minh \[CA\] là phân giác \(\widehat {MCK}\).
c) Kẻ \[Ax\] là tiếp tuyến của nửa đường tròn tại\[A\]. Lấy \(P \in Ax\) sao cho \(\frac{{AP.MB}}{{MA}} = R\).
Chứng minh \[PB\] đi qua trung điểm của đoạn thẳng\[HK\].
a) Gọi \[I\] là trung điểm của \[HB\]\( \Rightarrow HI = IB = \frac{{HB}}{2}\)
Xét nửa đường tròn \((O)\), đường kính \[AB\] có: \(\widehat {ACB} = 90^\circ \) (góc nội tiếp chắn nửa đường tròn)
\( \Rightarrow \Delta CHB\) vuông, mà \[CI\] là đường trung tuyến
\( \Rightarrow IC = IH = IB = \frac{{HB}}{2}\) (1)
Xét nửa đường tròn \((O)\), đường kính \[AB\] có: \(\widehat {HKB} = 90^\circ \) (góc nội tiếp chắn nửa đường tròn)
\( \Rightarrow \Delta KHB\) vuông, mà \[KI\] là đường trung tuyến.
\( \Rightarrow IK = IH = IB = \frac{{HB}}{2}\) (2)
Từ (1) và (2) suy ra: \( \Rightarrow IC = IK = IH = IB\)
\( \Rightarrow \) Bốn điểm \[C,{\rm{ }}B,{\rm{ }}H,{\rm{ }}K\]cùng thuộc một đường tròn.
b) Có \(\widehat {MCA} = \widehat {MBA}\) (góc nội tiếp cùng chắn ); \(\widehat {ACK} = \widehat {MBA}\) (tứ giác \(CHKB\) nội tiếp)
\( \Rightarrow \widehat {MCA} = \widehat {ACK}\)
\( \Rightarrow CA\) là phân giác \(\widehat {MCK}\).
c) Theo giả thiết: \(\frac{{AP.MB}}{{MA}} = R\)\( \Rightarrow \frac{{AP}}{{MA}} = \frac{{OA}}{{MB}}\)
Xét \(\Delta PAO\) và \(\Delta AMB\) có: \(\frac{{AP}}{{MA}} = \frac{{OA}}{{MB}}\); \(\widehat {PAO} = \widehat {AMB} = 90^\circ \)
(c-g-c)
\( \Rightarrow \widehat {POA} = \widehat {MBA}\) (hai góc tương ứng)
\[ \Rightarrow OP{\rm{ // B}}Q\]
Xét \(\Delta ABQ\) có: \[OP{\rm{ // B}}Q\], \[O\]là trung điểm của AB nên \[P\]là trung điểm của \[AQ\].
Gọi \[F\]là giao điểm của \[BP\] và \[HK\].
Xét \(\Delta ABP\)có \[FK{\rm{ // }}AP\]nên \[\frac{{FK}}{{AP}} = \frac{{BF}}{{BP}}\]
Xét \(\Delta QBP\)có \[FH{\rm{ // }}QP\]nên \[\frac{{FH}}{{QP}} = \frac{{BF}}{{BP}}\]
Từ đó \(HF = FK\)suy ra \[PB\] đi qua trung điểm của đoạn thẳng\[HK\].
Hot: 1000+ Đề thi cuối kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Gọi \(a,b(cm)(a > 0,b > 0)\) là độ dài chiều dọc và chiều ngang của trang chữ suy ra kích thước trang giấy là \(a + 6,b + 4.\)
Ta có: \(a.b = 384\) suy ra \(b = \frac{{384}}{a}(1)\).
Diện tích trang sách là \(S = (a + 6)(b + 4)\)
Suy ra \(S = 4a + \frac{{2304}}{a} + 408\).
Theo bất đẳng thức CAUCHY ta có:
\(S \ge 2\sqrt {4a.\frac{{2304}}{a}} + 408 = 600.\)
Suy ra \(MinS = 600\)suy ra \(4a = \frac{{2304}}{a}\)suy ra \(a = 24\)
Suy ra chiều dọc và chiều ngang tối ưu của trang giấy là\(30cm,20cm\).
Lời giải
Gọi giá tiền niêm yết của một cái bàn ủi:\(x\) (ngàn đồng).
Gọi giá tiền niêm yết của một cái quạt điện là: \(y\) (ngàn đồng).
Điều kiện: \(0 < x < 850;\,\,0 < y < 850\).
Vì với tổng số tiền theo giá niêm yết là \(850\) ngàn đồng nên ta có phương trình:
\(x + y = 850\). (1)
Thực tế khi trả tiền:
+ Số tiền mà anh Bình được giảm khi mua một cái bàn ủi là: \(10\% \,x = 0,1x\) (ngàn đồng).
+ Số tiền mà anh Bình được giảm khi mua một cái quạt điện là: \(20\% \,y = 0,2y\) (ngàn đồng).
Vì anh Bình đã được giảm giá \(125\) ngàn đồng khi mua \(2\) sản phẩm trên nên ta có phương trình: \(0,1\,x + 0,2\,y\, = 125\). \(\left( 2 \right)\)
Từ \(\left( 1 \right)\) và \(\left( 2 \right)\) ta có hệ phương trình: \(\left\{ \begin{array}{l}x + y = 850\\0,1\,x + 0,2\,y\, = 125\end{array} \right.\).
Giải hệ phương trình ta được: \(\left\{ \begin{array}{l}x = 450\\y = 400\end{array} \right.\) (thỏa mãn điều kiện).
Vậy số tiền chênh lệch giữa giá bán niêm yết với giá bán thực tế của một chiếc bàn ủi mà anh Bình đã mua là: \(450\;.\;10\% = 45\) (ngàn).
Số tiền chênh lệch giữa giá bán niêm yết với giá bán thực tế của một chiếc bàn ủi mà anh Bình đã mua là: \(400\;.\;20\% = 80\) (ngàn).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.