III. Lời giải chi tiết tự luận
(1,5 điểm)
1. Tính giá trị của biểu thức \(P = \frac{{{6^{3 + \sqrt 5 }}}}{{{2^{2 + \sqrt 5 }} \cdot {3^{1 + \sqrt 5 }}}}\).
III. Lời giải chi tiết tự luận
(1,5 điểm)
1. Tính giá trị của biểu thức \(P = \frac{{{6^{3 + \sqrt 5 }}}}{{{2^{2 + \sqrt 5 }} \cdot {3^{1 + \sqrt 5 }}}}\).
Câu hỏi trong đề: Bộ 10 đề thi giữa kì 2 Toán 11 Cánh diều có đáp án !!
Quảng cáo
Trả lời:
Ta có \(P = \frac{{{6^{3 + \sqrt 5 }}}}{{{2^{2 + \sqrt 5 }} \cdot {3^{1 + \sqrt 5 }}}} = \frac{{{{\left( {2 \cdot 3} \right)}^{3 + \sqrt 5 }}}}{{{2^{2 + \sqrt 5 }} \cdot {3^{1 + \sqrt 5 }}}} = \frac{{{2^{3 + \sqrt 5 }} \cdot {3^{3 + \sqrt 5 }}}}{{{2^{2 + \sqrt 5 }} \cdot {3^{1 + \sqrt 5 }}}}\)
\( = {2^{\left( {3 + \sqrt 5 } \right) - \left( {2 + \sqrt 5 } \right)}} \cdot {3^{\left( {3 + \sqrt 5 } \right) - \left( {1 + \sqrt 5 } \right)}} = {2^1} \cdot {3^2} = 18.\)
Câu hỏi cùng đoạn
Câu 2:
2. Cho \[a = {\log _2}3;b = {\log _3}5;c = {\log _7}2.\] Tính giá trị của \[{\log _{140}}63\] theo \(a,\,b,\,c\).
2. Cho \[a = {\log _2}3;b = {\log _3}5;c = {\log _7}2.\] Tính giá trị của \[{\log _{140}}63\] theo \(a,\,b,\,c\).
2. (0,5 điểm)
Ta có \[{\log _{140}}63 = \frac{{{{\log }_2}63}}{{{{\log }_2}140}} = \frac{{{{\log }_2}\left( {{3^2} \cdot 7} \right)}}{{{{\log }_2}\left( {{2^2} \cdot 5 \cdot 7} \right)}} = \frac{{2{{\log }_2}3 + {{\log }_2}7}}{{2 + {{\log }_2}5 + {{\log }_2}7}}\]
\[ = \frac{{2{{\log }_2}3 + \frac{1}{{{{\log }_7}2}}}}{{2 + {{\log }_2}3 \cdot {{\log }_3}5 + \frac{1}{{{{\log }_7}2}}}} = \frac{{2a + \frac{1}{c}}}{{2 + ab + \frac{1}{c}}}\]
\[ = \frac{{1 + 2ac}}{{1 + 2c + abc}}.\]
Câu 3:
3. Năm \(2023\), một hãng xe ô tô niêm yết giá bán loại xe \(X\) là \(750\,\,000\,\,000\) đồng và dự định trong \(10\) năm tiếp theo, mỗi năm giảm \(1,8\% \) giá bán của năm liền trước. Theo dự định đó, năm \(2030\) hãng xe ô tô niêm yết giá bán xe \(X\) là bao nhiêu (kết quả làm tròn đến hàng nghìn)?
3. Năm \(2023\), một hãng xe ô tô niêm yết giá bán loại xe \(X\) là \(750\,\,000\,\,000\) đồng và dự định trong \(10\) năm tiếp theo, mỗi năm giảm \(1,8\% \) giá bán của năm liền trước. Theo dự định đó, năm \(2030\) hãng xe ô tô niêm yết giá bán xe \(X\) là bao nhiêu (kết quả làm tròn đến hàng nghìn)?
3. (0,5 điểm)
Giá bán xe năm đầu tiên: \[{A_1} = 750\,\,000\,\,000\] đồng.
Giá bán xe năm thứ hai: \({A_2} = {A_1} - {A_1} \cdot r = {A_1}\left( {1 - r} \right)\) đồng, với \(r = 1,8\% \).
Giá bán xe năm thứ ba: \({A_3} = {A_2} - {A_2}r = {A_2}\left( {1 - r} \right) = {A_1}{\left( {1 - r} \right)^2}\) đồng.
…
Giá bán xe năm thứ \(n\): \({A_n} = {A_1}{\left( {1 - r} \right)^{n - 1}}\) đồng.
Vậy giá bán xe năm thứ 8 (năm 2030) là:
\({A_6} = {A_1}{\left( {1 - r} \right)^7} = 750\,\,000\,\,000{\left( {1 - 1,8\% } \right)^7} \approx 660\,\,453\,\,000\) đồng.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Sách - Sổ tay kiến thức trọng tâm Vật lí 11 VietJack - Sách 2025 theo chương trình mới cho 2k8 ( 45.000₫ )
- Trọng tâm Hóa học 11 dùng cho cả 3 bộ sách Kết nối, Cánh diều, Chân trời sáng tạo VietJack - Sách 2025 ( 58.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
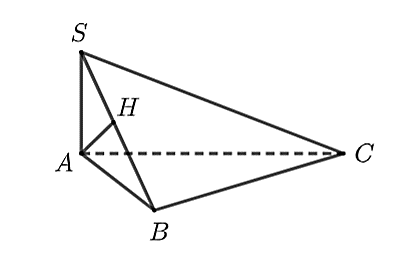
a) Vì \(SA \bot \left( {ABC} \right)\) nên \(SA \bot BC\).
Lại có \(BC \bot AB\) (do tam giác \(ABC\) vuông tại \(B\)).
Từ đó suy ra \(BC \bot \left( {SAB} \right)\).
Câu 2
Lời giải
Đáp án đúng là: A
Ta có bảng sau:
|
Doanh thu |
\(\left[ {5;7} \right)\) |
\(\left[ {7;9} \right)\) |
\(\left[ {9;11} \right)\) |
\(\left[ {11;13} \right)\) |
\(\left[ {13;15} \right)\) |
|
Giá trị đại diện |
6 |
8 |
10 |
12 |
14 |
|
Số ngày |
2 |
7 |
7 |
3 |
1 |
Số trung bình của mẫu số liệu là \(\overline x = \frac{{2.6 + 7.8 + 7.10 + 3.12 + 1.14}}{{20}} = 9,4.\)
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.