(4,0 điểm)
Mặt xung quanh của một thùng chứa nước hình trụ có chiều cao \(1m\) được gõ từ một tấm tôn hình chữ nhật có kích thước \[1m\] x\[2m\] (như hình vẽ).
Mặt xung quanh của một thùng chứa nước hình trụ có chiều cao \(1m\) được gõ từ một tấm tôn hình chữ nhật có kích thước \[1m\] x\[2m\] (như hình vẽ).
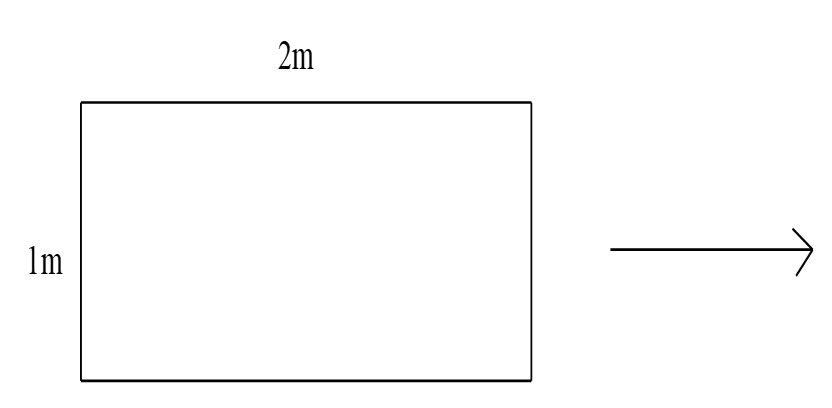
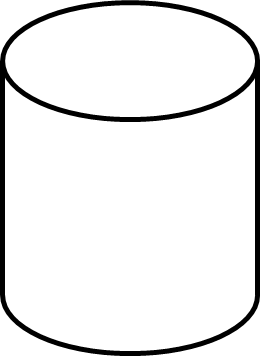
a) Hỏi thùng nước này đựng đầy được bao nhiêu mét khối nước?
(Bỏ qua bề dày của thùng nước và lấy \[\pi = 3,14\] làm tròn đến chữ số thập phân thứ hai).
b) Một em bé đánh rơi quả bóng bưởi xuống thùng tôn. Bên cạnh có một vòi nước cung cấp nước. Em bé cần lấy ít nhất bao nhiêu nước từ vòi để lấy được bóng bưởi một cách an toàn?
Quảng cáo
Trả lời:
Gọi \(R\) là bán kính đáy của hình trụ
Ta có : \(C = 2\pi R \Leftrightarrow R = \frac{C}{{2\pi }} = \frac{2}{{2\pi }} = \frac{1}{\pi }\) \((m)\)
Thể tích của hình trụ là : \(V = \pi {R^2}h = \pi .{\left( {\frac{1}{\pi }} \right)^2}.1 = \pi .\frac{1}{{{\pi ^2}}} = \frac{1}{\pi } = \frac{1}{{3,14}} \approx 0,32{m^3}\)
Vậy thùng đựng được \(0,32{m^3}\) nước.
b) Để lấy bóng, em bé chỉ cần đổ đầy nước vào thùng tôn. Em bé cần lấy ít nhất \(0,32{m^3}\) nước.
Thì bóng nổi trên mặt thùng tôn khi đó sẽ an toàn.
Câu hỏi cùng đoạn
Câu 2:
Cho đường tròn \(\left( {O;R} \right)\)có hai đường kính \(AB\)và \(CD\) vuông góc tại \(O\). Gọi I là trung điểm của \(OB\). Tia \(CI\) cắt đường tròn \(\left( O \right)\) tại \(E\). Gọi \(H\) là giao điểm của \(AE\) và \(CD\).
a) Chứng minh bốn điểm \(O\), \(I\), \(E\), \(D\) cùng thuộc một đường tròn.
b) Chứng minh: \[AH.\,AE = 2{R^2}\] và\(OA = 3 \cdot OH\).
c) Gọi \(K\) là hình chiếu của \(O\) trên \(BD\), \(Q\) là giao điểm của \(AD\) và \(BE\).
Chứng minh: \(Q,\,K,\,I\)thẳng hàng.
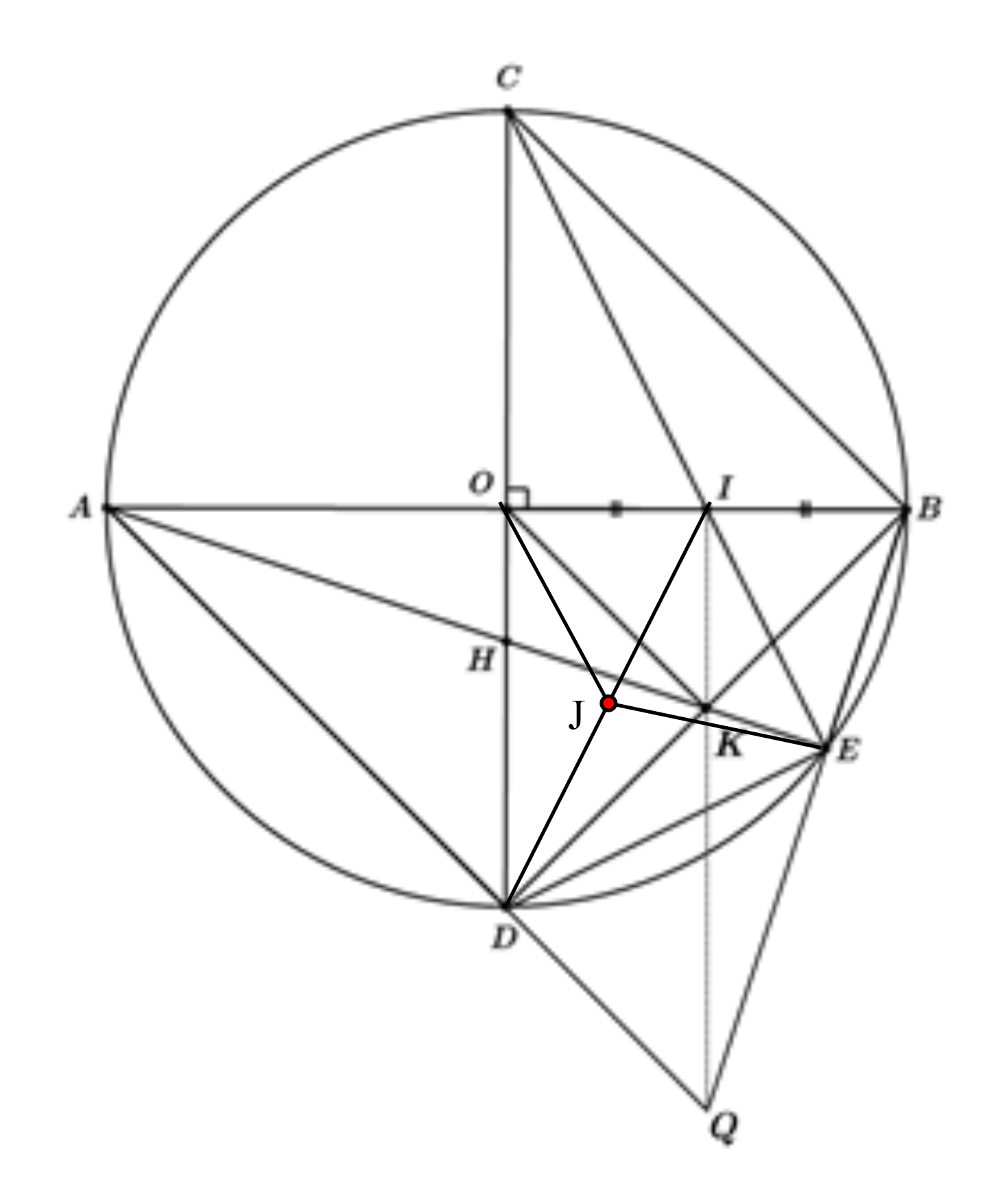
Cho đường tròn \(\left( {O;R} \right)\)có hai đường kính \(AB\)và \(CD\) vuông góc tại \(O\). Gọi I là trung điểm của \(OB\). Tia \(CI\) cắt đường tròn \(\left( O \right)\) tại \(E\). Gọi \(H\) là giao điểm của \(AE\) và \(CD\).
a) Chứng minh bốn điểm \(O\), \(I\), \(E\), \(D\) cùng thuộc một đường tròn.
b) Chứng minh: \[AH.\,AE = 2{R^2}\] và\(OA = 3 \cdot OH\).
c) Gọi \(K\) là hình chiếu của \(O\) trên \(BD\), \(Q\) là giao điểm của \(AD\) và \(BE\).
Chứng minh: \(Q,\,K,\,I\)thẳng hàng.

a) Gọi \(J\) là trung điểm của \(ID\)
+) \(AB \bot CD\) tại \(O\), mà \(I \in OB\)
Suy ra \[\widehat {IOD} = {90^0}\]\[ \Rightarrow \Delta IOD\]vuông tại \(O\),
từ đó suy ra \[JO = JI = JD\](1)
+) Chứng minh: \[\widehat {IED} = {90^0}\]\[ \Rightarrow \Delta IED\]vuông tại \(E\),
từ đó suy ra JI = JE = JD (2)
+) Từ (1) và (2) suy ra O, I, E, D cùng thuộc một đường tròn
b) +) Chứng minh: \[\Delta AHO\# \Delta ABE\] (g.g)
+) Suy ra: \[AH \cdot AE = AO \cdot AB = R \cdot 2R = 2{R^2}\]
+) Suy ra: \[\frac{{OA}}{{OH}} = \frac{{AE}}{{BE}}\]
+) Mà \(EI\) là tia phân giác của góc \(AEB\) nên suy ra:
\[\frac{{AE}}{{BE}} = \frac{{AI}}{{IB}} = \frac{{\frac{3}{2}R}}{{\frac{1}{2}R}} = 3\]
+) Suy ra: \[\frac{{OA}}{{OH}} = 3\], do đó \[OA = 3.OH\]
c) +) Chứng minh được: \[OD = 3.OH\] suy ra \[HD = \frac{2}{3}OD\]
+) Suy ra: \(H\) là trọng tâm \[\Delta ABD\]
+) Chứng minh \(K\) là trung điểm của \(BD\)
Suy ra: \(A,\,H,\,K,\,E\) thẳng hàng
+) Suy ra: \(K\) là trực tâm của \[\Delta ABQ\]
+) Suy ra: \(KQ\) vuông góc \(AB\)
+) Chứng minh được: \(KI\) vuông góc \(AB\)
+) Suy ra: \(Q,\,K,\,I\) thẳng hàng
Hot: 1000+ Đề thi cuối kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Gọi khối lượng dung dịch \(X\) và \(Y\) lần lượt là \(x,\,y\)( g) điều kiện \(x > 0,y > 0\)
Nồng độ muối trong dung dịch \(X\) là \(\frac{5}{x} \cdot 100\% \)
Nồng độ muối trong dung dịch \(Y\) là \(\frac{{4,8}}{x} \cdot 100\% \)
Khối lượng hai dung dịch là \(220\) gam nên \(x + y = 220\)(g) (1)
Nồng độ muối trong dung dịch \(X\) nhiêu hơn nồng độ muối trong dung dịch \(Y\) là \(1\% \) nên
\(\frac{5}{x}.100\% - \frac{{4,8}}{y}.100\% = 1\% \) (2)
Từ (1) và (2) ta có hệ \(\left\{ \begin{array}{l}x + y = 220\\\frac{5}{x}.100\% - \frac{{4,8}}{y}.100\% = 1\% \end{array} \right.\)
Suy ra \(x = 100,y = 120\)
Vậy khối lượng dung dịch \(X\) và \(Y\) lần lượt là \({\rm{100(g)}}{\rm{,120(g)}}\)
Lời giải
Thay \(x = 36\)(tmđk) vào \(A\) ta được \(A = \frac{{36 - 5}}{{\sqrt {36} }} = \frac{{31}}{6}\)
Vậy \(A = \frac{{31}}{6}\)khi \(x = 36\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.