(4,0 điểm)
Để làm một mô hình cái bút chì trang trí, người ta dùng một khối gỗ hình trụ và một khối gỗ hình nón có cùng đường kính đáy chồng khít lên nhau. Khối gỗ hình trụ có đường kính đáy là \(20cm\), chiều cao là \(30cm\). Khối gỗ hình nón có chiều cao là \(15cm\). Tính thể tích gỗ cần dùng để làm mô hình này.
Để làm một mô hình cái bút chì trang trí, người ta dùng một khối gỗ hình trụ và một khối gỗ hình nón có cùng đường kính đáy chồng khít lên nhau. Khối gỗ hình trụ có đường kính đáy là \(20cm\), chiều cao là \(30cm\). Khối gỗ hình nón có chiều cao là \(15cm\). Tính thể tích gỗ cần dùng để làm mô hình này.
Câu hỏi trong đề: Đề luyện thi Toán vào lớp 10 Hà Nội 2026 có đáp án - Đề 11 !!
Quảng cáo
Trả lời:
Vì đường kính của khôi gỗ hình trụ là \(20cm\) nên bán kính của khối gỗ hình trụ là \(10cm\).
Thể tích của khối gỗ hình trụ là: \(\pi {.10^2}.30 = 3000\pi \left( {c{m^3}} \right)\).
Thể tích của hình nón là: \(\frac{1}{3}\pi {.10^2}.15 = 500\pi \left( {c{m^3}} \right)\).
Thể tích gỗ cần dùng để làm mô hình này là: \(3000\pi + 500\pi = 3500\pi \left( {c{m^3}} \right)\)
Câu hỏi cùng đoạn
Câu 2:
Cho đường tròn \(\left( O \right)\), dây \(CD\) cố định. Gọi \(B\) là điểm chính giữa cung nhỏ \(CD\), kẻ đường kính \(AB\) cắt \(CD\) tại \(I\). Lấy điểm \(H\) bất kỳ trên cung lớn \(CD\), \(HB\) cắt \(CD\) tại \(E\). Đường thẳng \(AH\) cắt đường thẳng \(CD\) tại \(P\).
a) . Chứng minh: Tứ giác \(PHIB\) nội tiếp.
b). Chứng minh: \(AH.AP = AI.AB\).
c). Gọi \(K\) là giao điểm của đường thẳng \(AE\) và \(BP\). Kẻ \(KM \bot AB\) cắt \(AB\) tại \(M\), cắt đường tròn \(\left( O \right)\) tại \(N\) . Chứng minh \(N,I,H\) thẳng hàng.
Cho đường tròn \(\left( O \right)\), dây \(CD\) cố định. Gọi \(B\) là điểm chính giữa cung nhỏ \(CD\), kẻ đường kính \(AB\) cắt \(CD\) tại \(I\). Lấy điểm \(H\) bất kỳ trên cung lớn \(CD\), \(HB\) cắt \(CD\) tại \(E\). Đường thẳng \(AH\) cắt đường thẳng \(CD\) tại \(P\).
a) . Chứng minh: Tứ giác \(PHIB\) nội tiếp.
b). Chứng minh: \(AH.AP = AI.AB\).
c). Gọi \(K\) là giao điểm của đường thẳng \(AE\) và \(BP\). Kẻ \(KM \bot AB\) cắt \(AB\) tại \(M\), cắt đường tròn \(\left( O \right)\) tại \(N\) . Chứng minh \(N,I,H\) thẳng hàng.

a) . Chứng minh: Tứ giác \(PHIB\) nội tiếp.
Ta có \(\widehat {AHB} = 90^\circ \) (góc nội tiếp chắn nửa đường tròn) \( \Rightarrow \widehat {PHB} = 90^\circ \) (kề bù với \(\widehat {AHB} = 90^\circ \)); \(\widehat {PIB} = 90^\circ \) (GT) \( \Rightarrow H,I\) cùng thuộc đường tròn đường kính \(PB \Rightarrow \) tứ giác \(PHIB\) nội tiếp đường tròn đường kính \(PB\).
b) . Chứng minh: \(AH.AP = AI.AB\).
Xét \(\Delta AHI\) và \(\Delta ABP\) có:
\(\widehat {HAI}\) chung;
\(\widehat {AHI} = \widehat {ABP}\) (cùng bù với \(\widehat {PHI}\) do tứ giác \(PHIB\) nội tiếp)
.
c) . Gọi \(K\) là giao điểm của đường thẳng \(AE\) và \(BP\). Kẻ \(KM \bot AB\) cắt \(AB\) tại \(M\), cắt đường tròn \(\left( O \right)\) tại \(N\) . Chứng minh \(N,I,H\) thẳng hàng.
Tứ giác \(PHIB\) nội tiếp nên \(\widehat {HIP} = \widehat {HBP}\) (hai góc nội tiếp cùng chắn ) (1);
Tam giác \(ABP\) có hai đường cao \(PI,BH\) cắt nhau tại \(E \Rightarrow E\) là trực tâm của \(\Delta ABP \Rightarrow AE \bot BP\) hay \(AK \bot BP \Rightarrow \widehat {EKB} = 90^\circ \), mà \(\widehat {EIB} = 90^\circ \) (GT)\( \Rightarrow \) tứ giác \(BKEI\) nội tiếp đường tròn đường kính \(BE\) \( \Rightarrow \widehat {EIK} = \widehat {HBP}\) (hai góc nội tiếp cùng chắn ) (2);
Mà \(\widehat {EKB} = 90^\circ \)\( \Rightarrow K \in \left( O \right)\), lại có \(AB \bot KN\) tại \(M\) \( \Rightarrow MK = MN\)(quan hệ vuông góc đường kính và dây) \( \Rightarrow \Delta IMK = \Delta IMN\left( {c.g.c} \right)\) \( \Rightarrow \widehat {MIK} = \widehat {MIN} \Rightarrow 90^\circ - \widehat {MIK} = 90^\circ - \widehat {MIN}\) \( \Rightarrow \widehat {EIK} = \widehat {DIN}\)(3);
Từ (1), (2), (3) ta có \(\widehat {HIP} = \widehat {DIN}\left( { = \widehat {HBP} = \widehat {EIK}} \right) \Rightarrow \widehat {HIP} + \widehat {PIN} = \widehat {DIN} + \widehat {PIN} = \widehat {PID} = 180^\circ \)
\( \Rightarrow \widehat {HIN} = 180^\circ \Rightarrow H,I,N\) thẳng hàng.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
1) . Thay \(x = 64\) ( thỏa mãn điều kiện) vào biểu thức \(A\) ta được \(A = \frac{2}{{\sqrt {64} - 2}} = \frac{1}{3}\).
2) . Ta có \(B = \frac{{3\left( {\sqrt x + 2} \right) + \left( {\sqrt x - 2} \right)\left( {\sqrt x + 1} \right) + 2\sqrt x }}{{\left( {\sqrt x - 2} \right)\left( {\sqrt x + 2} \right)}} = \frac{{x + 4\sqrt x + 4}}{{\left( {\sqrt x - 2} \right)\left( {\sqrt x + 2} \right)}} = \frac{{\sqrt x + 2}}{{\sqrt x - 2}}\).
3) . Với \(x \ge 0, x \ne 4\) thì
\(P = \frac{A}{B} = \frac{2}{{\sqrt x - 2}}:\frac{{\sqrt x + 2}}{{\sqrt x - 2}} = \frac{2}{{\sqrt x + 2}}\).
Để
\(P \ge \frac{2}{{x + 2}} \Rightarrow \frac{2}{{\sqrt x + 2}} \ge \frac{2}{{x + 2}}\).
Do \(2 > 0\) và \(x + 2 > 0, \sqrt x + 2 > 0 \Rightarrow \sqrt x + 2 \le x + 2 \Rightarrow \sqrt x \left( {\sqrt x - 1} \right) \ge 0\)
TH1: \(\sqrt x \left( {\sqrt x - 1} \right) = 0\) nên \(\sqrt x = 0 \Rightarrow x = 0\) (
TH2: \(\sqrt x \left( {\sqrt x - 1} \right) > 0 \Rightarrow \sqrt x - 1 > 0\) vì \(\sqrt x \ge 0\) nên \(x > 1\).
Kết hợp với điều kiện \(x \ge 0, x \ne 4\) ta được \(x = 0\) hoặc \(x \ge 1, x \ne 4\).
Lời giải
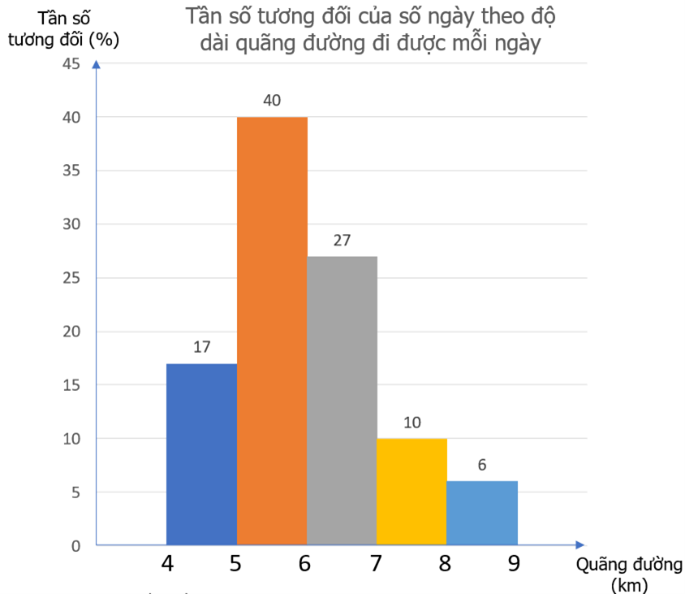
Nhóm có tần số tương đối ghép nhóm lớn nhất là \([5;6)\)có tần số tương đối \(f = 40\% \)
và tần số \(n = 12\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.