(0,5 điểm) Một công ty sản xuất dụng cụ thể thao nhận được một đơn đặt hàng sản xuất \(8000\) quả bóng tennis. Công ty này sở hữu một số máy móc, mỗi máy móc có thể sản xuất \(30\) quả bóng trong một giờ. Chi phí thiết lập các máy này là \(200\) nghìn đồng cho mỗi máy. Khi được thiết lập, hoạt động sản xuất sẽ hoàn toàn diễn ra tự động dưới sự giám sát. Số tiền phải trả cho người giám sát là \(192\) nghìn đồng một giờ (người này sẽ giám sát tất cả các máy hoạt động). Số máy móc công ty nên sử dụng là bao nhiêu để chi phí sản xuất là thấp nhất?

 1) . Thay \(x = 64\) ( thỏa mãn điều kiện) vào biểu thức \(A\) ta được \(A = \frac{2}{{\sqrt {64}  - 2}} = \frac{1}{3}\).

 2) . Ta có \(B = \frac{{3\left( {\sqrt x  + 2} \right) + \left( {\sqrt x  - 2} \right)\left( {\sqrt x  + 1} \right) + 2\sqrt x }}{{\left( {\sqrt x  - 2} \right)\left( {\sqrt x  + 2} \right)}} = \frac{{x + 4\sqrt x  + 4}}{{\left( {\sqrt x  - 2} \right)\left( {\sqrt x  + 2} \right)}} = \frac{{\sqrt x  + 2}}{{\sqrt x  - 2}}\).

3) . Với \(x \ge 0,  x \ne 4\) thì

 \(P = \frac{A}{B} = \frac{2}{{\sqrt x  - 2}}:\frac{{\sqrt x  + 2}}{{\sqrt x  - 2}} = \frac{2}{{\sqrt x  + 2}}\).

Để

\(P \ge \frac{2}{{x + 2}} \Rightarrow \frac{2}{{\sqrt x  + 2}} \ge \frac{2}{{x + 2}}\).

Do \(2 > 0\) và \(x + 2 > 0,  \sqrt x  + 2 > 0 \Rightarrow \sqrt x  + 2 \le x + 2 \Rightarrow \sqrt x \left( {\sqrt x  - 1} \right) \ge 0\)

TH1: \(\sqrt x \left( {\sqrt x  - 1} \right) = 0\) nên \(\sqrt x  = 0 \Rightarrow x = 0\) (

TH2: \(\sqrt x \left( {\sqrt x  - 1} \right) > 0 \Rightarrow \sqrt x  - 1 > 0\) vì \(\sqrt x  \ge 0\) nên \(x > 1\).

Kết hợp với điều kiện \(x \ge 0,  x \ne 4\) ta được \(x = 0\) hoặc \(x \ge 1,  x \ne 4\).

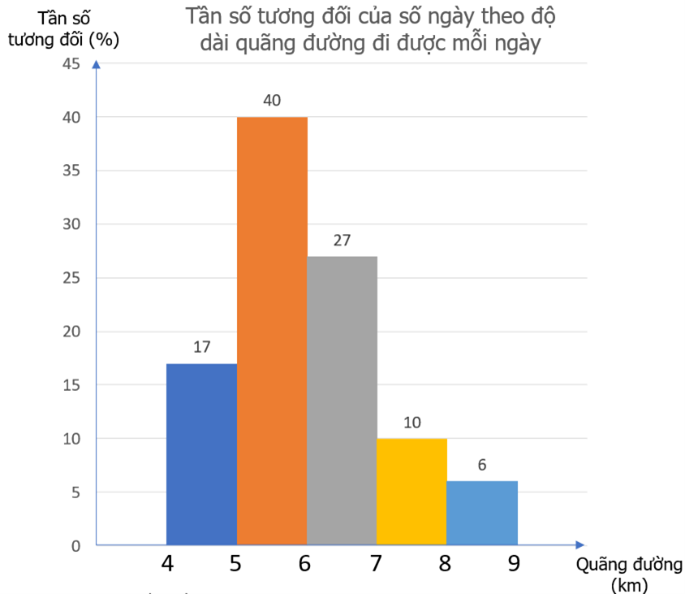
Nhóm có tần số tương đối ghép nhóm lớn nhất là \([5;6)\)có tần số tương đối \(f = 40\% \)

và tần số \(n = 12\).