(2,5 điểm)

Nhân dịp ngày Giỗ Tổ Hùng Vương, một siêu thị điện máy đã giảm giá nhiều mặt hàng để kích cầu mua sắm. Giá niêm yết của một chiếc tủ lạnh và một chiếc máy giặt có tổng số tiền là 25,4 triệu đồng. Tuy nhiên, trong dịp này tủ lạnh giảm 40% giá niêm yết và máy giặt giảm 25% giá niêm yết. Vì thế, cô Liên đã mua hai mặt hàng trên với tổng số tiền là 16,77 triệu đồng. Hỏi giá niêm yết của mỗi mặt hàng trên là bao nhiêu?

(1,5 điểm) Cho hai biểu thức \(A = \frac{2}{{\sqrt x  - 2}}\) và \(B = \frac{3}{{\sqrt x  - 2}} + \frac{{\sqrt x  + 1}}{{\sqrt x  + 2}} - \frac{{2\sqrt x }}{{4 - x}}\) với \(x \ge 0,  x \ne 4\)

1) . Tính giá trị của biểu thức \(A\) khi \(x = 64\)

2) . Chứng minh rằng \(B = \frac{{\sqrt x  + 2}}{{\sqrt x  - 2}}\)

3) . Cho \(P = \frac{A}{B}\). Tìm các giá trị của \(x\) để \(P \ge \frac{2}{{x + 2}}\)

Nam thống kê lại độ dài quãng đường (đơn vị: km) mình đi bộ mỗi ngày trong tháng 9 và biểu diễn dưới dạng biểu đồ tần số tương đối ghép nhóm sau:

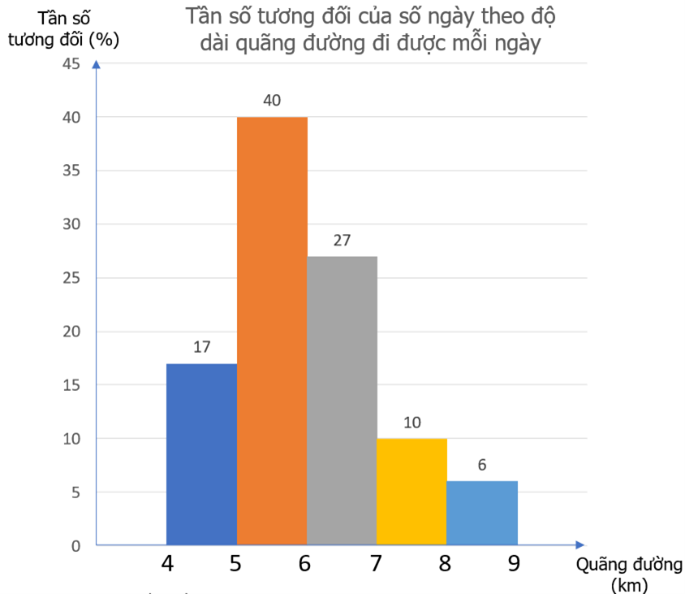
Tìm nhóm có tần số tương đối ghép nhóm lớn nhất. Xác định  tần số và tần số tương đối ghép nhóm của nhóm đó.

Để làm một mô hình cái bút chì trang trí, người ta dùng một khối gỗ hình trụ và một khối gỗ hình nón có cùng đường kính đáy chồng khít lên nhau. Khối gỗ hình trụ có đường kính đáy là \(20cm\), chiều cao là \(30cm\). Khối gỗ hình nón có chiều cao là \(15cm\). Tính thể tích gỗ cần dùng để làm mô hình này.

(0,5 điểm) Một công ty sản xuất dụng cụ thể thao nhận được một đơn đặt hàng sản xuất \(8000\) quả bóng tennis. Công ty này sở hữu một số máy móc, mỗi máy móc có thể sản xuất \(30\) quả bóng trong một giờ. Chi phí thiết lập các máy này là \(200\) nghìn đồng cho mỗi máy. Khi được thiết lập, hoạt động sản xuất sẽ hoàn toàn diễn ra tự động dưới sự giám sát. Số tiền phải trả cho người giám sát là \(192\) nghìn đồng một giờ (người này sẽ giám sát tất cả các máy hoạt động). Số máy móc công ty nên sử dụng là bao nhiêu để chi phí sản xuất là thấp nhất?