(1,5 điểm)
Hệ thống đăng kiểm quốc gia ghi nhận 2000 xe ô tô của cùng 1 loại xe tới đăng kiểm. Người ta thu được biểu đồ tần số ghép nhóm về số năm sử dụng tốt mà chưa phải sửa chữa lớn của xe như dưới đây
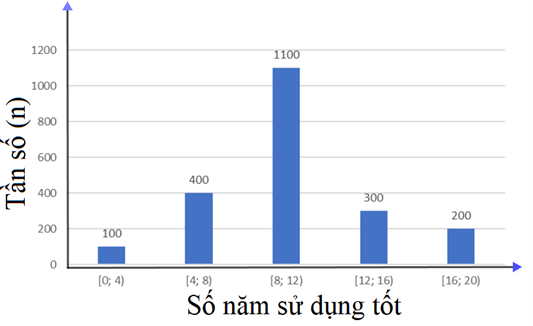
Tìm tần số ghép nhóm và tần số tương đối ghép nhóm của nhóm [8; 12)
(1,5 điểm)
Hệ thống đăng kiểm quốc gia ghi nhận 2000 xe ô tô của cùng 1 loại xe tới đăng kiểm. Người ta thu được biểu đồ tần số ghép nhóm về số năm sử dụng tốt mà chưa phải sửa chữa lớn của xe như dưới đây
Tìm tần số ghép nhóm và tần số tương đối ghép nhóm của nhóm [8; 12)
Quảng cáo
Trả lời:
Giải bởi Vietjack
Từ biểu đồ ta có nhóm [8; 12) có tần số ghép nhóm là 1100
(nghĩa là có 1100 xe loại đó được sử dụng tốt từ 8 tới dưới 12 năm mới phải thực hiện đại tu lần đầu trong 4 năm sử dụng tiếp theo)
Tần số tương đối ghép nhóm là \(\frac{{1100}}{{2000}}.100\% = 55\% \)
(nghĩa là có 55% số xe loại đó sử dụng tốt từ 8 tới 12 năm, sau đó các xe này đều phải đại tu, sửa chữa hoặc thay thế trong 4 năm sử dụng tiếp theo.
Câu hỏi cùng đoạn
Câu 2:
Bạn An là một thành viên của câu lạc bộ nhảy hiện đại khối 9 trong trường THCS. Để chọn học sinh trong CLB đó tham gia hoạt động văn nghệ chào mừng “Ngày nhà giáo Việt Nam” của trường, các học sinh trong CLB sử dụng hình thức bốc thăm với 20 lá thăm giống hệt nhau lần lượt ghi các số tự nhiên từ 1 tới 20 và được để trong hộp kín. Học sinh lấy được lá thăm ghi số chia hết cho 6 sẽ được tham gia. Bạn An là người được bốc thăm đầu tiên.
Xét phép thử “Bạn An bốc ngẫu nhiên 1 lá thăm” và biến cố B: ”Bạn An được tham gia hoạt động văn nghệ chào mừng Ngày nhà giáo Việt Nam của trường”. Tính xác suất của biến cố B.
Bạn An là một thành viên của câu lạc bộ nhảy hiện đại khối 9 trong trường THCS. Để chọn học sinh trong CLB đó tham gia hoạt động văn nghệ chào mừng “Ngày nhà giáo Việt Nam” của trường, các học sinh trong CLB sử dụng hình thức bốc thăm với 20 lá thăm giống hệt nhau lần lượt ghi các số tự nhiên từ 1 tới 20 và được để trong hộp kín. Học sinh lấy được lá thăm ghi số chia hết cho 6 sẽ được tham gia. Bạn An là người được bốc thăm đầu tiên.
Xét phép thử “Bạn An bốc ngẫu nhiên 1 lá thăm” và biến cố B: ”Bạn An được tham gia hoạt động văn nghệ chào mừng Ngày nhà giáo Việt Nam của trường”. Tính xác suất của biến cố B.
Giải bởi Vietjack
Xét phép thử “Bạn An bốc ngẫu nhiên 1 lá thăm”.
Kết quả của phép thử là An rút được 1 lá thăm có ghi 1 số tự nhiên (trong khoảng từ 1 tới 20) từ trong hộp. Do các lá thăm giống nhau nên có 20 kết quả có thể đồng khả năng.
Biến cố B: ”Bạn An được tham gia hoạt động văn nghệ chào mừng Ngày nhà giáo Việt Nam của trường” tương ứng với việc An bốc được lá thăm có ghi số 6, hoặc số 12 hoặc số 18.
Do đó, có 3 kết quả thuận lợi của biến cố B.
Xác suất của biến cố B là \(P(B) = \frac{3}{{20}} = 15\% \)Hot: 1000+ Đề thi cuối kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Gọi số gam thịt bò và thịt heo cần sử dụng lần lượt là \[x;y\left( g \right)\] \[\left( {x > 0;y > 0} \right)\]
\[1\] gam thịt bò có chứa \[80:100 = 0,8\] (đv protein) và \[20:100 = 0,2\] (đv lipit)
\[1\] gam thịt heo có chứa \[60:100 = 0,6\](đv protein) và \[40:100 = 0,4\] (đv lipit)
Do cần đảm bảo đủ \[900\] đơn vị protein nên ta có phương trình: \[0,8x + 0,6y = 900\left( 1 \right)\]
Do cần đảm bảo đủ \[400\] đơn vị lipit nên ta có phương trình: \[0,2x + 0,4y = 400\left( 2 \right)\]
Từ \(\left( 1 \right);\left( 2 \right)\) ta có hệ phương trình \[\left\{ \begin{array}{l}0,8x + 0,6y = 900\\0,2x + 0,4y = 400\end{array} \right.\]\[ \Rightarrow \left\{ \begin{array}{l}x = 600\left( {{\rm{t/m}}} \right)\\y = 700\left( {{\rm{t/m}}} \right)\end{array} \right.\]
Vậy số gam thịt bò và thịt heo người nội trợ cần sử dụng lần lượt là \[600g;\,\,700g.\]
Lời giải
a) Đổi: 3dm = 30cm; \(R = 30:2 = 15\,\left( {cm} \right)\);
Thể tích của thùng nước là: \(V = \pi {R^2}h\)
\( = \pi {.15^2}.36 = 8100\pi \approx 25447\,\left( {c{m^3}} \right)\)
b) Thể tích nước mỗi lần xách là: \(25447.90\% = 22902,3\left( {c{m^3}} \right) = 0,0229023\left( {{m^3}} \right)\)
Số thùng nước cần đổ để đầy bể là:\(1:0,0229023 \approx 43,66\) (thùng)
Vậy cần phải đổ ít nhất 44 thùng để đầy bể chứa.
Câu 3
(1,5 điểm) Cho hai biểu thức: \(A = \frac{{\sqrt x - 1}}{{\sqrt x }}\); \(B = \frac{{2\sqrt x }}{{\sqrt x + 3}} + \frac{4}{{\sqrt x - 3}} + \frac{{x - 4\sqrt x + 15}}{{9 - x}}\) với \(x > 0\,;\,x \ne 9\)
1) Tính giá trị của biểu thức A khi x = 25.
2) Chứng minh \(B = \frac{{\sqrt x - 1}}{{\sqrt x - 3}}\).
3) Cho P = A: B. Tìm x nguyên để \(\left| P \right| + P = 0\).
(1,5 điểm) Cho hai biểu thức: \(A = \frac{{\sqrt x - 1}}{{\sqrt x }}\); \(B = \frac{{2\sqrt x }}{{\sqrt x + 3}} + \frac{4}{{\sqrt x - 3}} + \frac{{x - 4\sqrt x + 15}}{{9 - x}}\) với \(x > 0\,;\,x \ne 9\)
1) Tính giá trị của biểu thức A khi x = 25.
2) Chứng minh \(B = \frac{{\sqrt x - 1}}{{\sqrt x - 3}}\).
3) Cho P = A: B. Tìm x nguyên để \(\left| P \right| + P = 0\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập