(4,0 điểm)      

Gạch ống là một sản phẩm được tạo hình thành từ đất sét và nước, được kết hợp lại với nhau theo một công thức chung hợp lý mới có thể tạo ra hỗn hợp dẻo quánh, sau đó chúng được đổ vào khuôn, rồi đem phơi hoặc sấy khô và cuối cùng là đưa vào lò nung. Một viên gạch hình hộp chữ nhật có kích thước dài \[20cm\], rộng \[8cm\]. Bên trong có bốn lỗ hình trụ bằng nhau có đường kính \[2,5cm\].

a.      Tính thể tích đất sét để làm một viên gạch. (lấy \(\pi  \approx 3,14\))

b.     Theo toán học, bác Ba muốn xây một ngôi nhà phải mua \[10\] thiên gạch, giá một viên là \[1{\rm{ }}100\] đồng. Nhưng khi thi công, bác Ba phải mua dư \[2\% \] số gạch cần dùng dự phòng cho hư hao. Tính số tiền bác Ba mua gạch để xây căn nhà, biết \[1\] thiên gạch là \[1{\rm{ }}000\] viên.

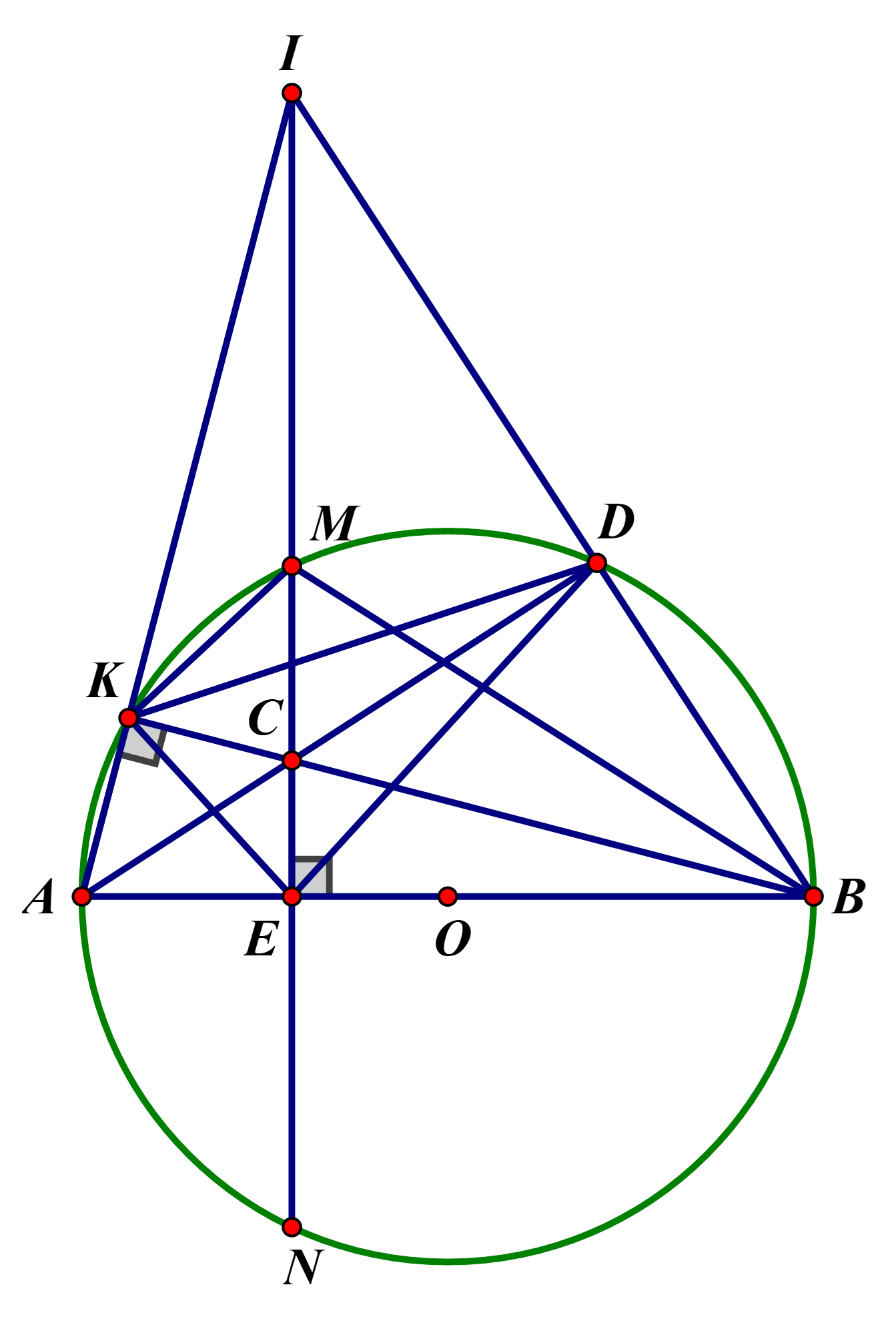
a. Ta có: \(\widehat {AKB} = {90^0}\) (Góc nội tiếp chắn nửa đường tròn \[\left( O \right)\])

nên \(\Delta AKC\) vuông tại \(K\)

Do đó, ba điểm \(A,K,C\) thuộc đường tròn đường kính \[AC\] (1)

+) Ta có \(\widehat {AEC} = {90^0}\) (vì đường kính \[AB\] vuông góc với dây \[MN\] tại \[E\] theo giả thiết)

Nên \(\Delta AEC\) vuông tại \(E\)

Do đó, ba điểm \(A,E,C\) thuộc đường tròn đường kính \[AC\] (2)

Từ (1) và (2), ta có bốn điểm \(A,K,E,C\) cùng thuộc đường tròn đường kính \(AC\)

Vậy tứ giác \[AKCE\]nội tiếp.

b. + Ta có tứ giác AKCE nội tiếp (cmt)

nên \(\widehat {KA{\rm{E}}} + \widehat {KC{\rm{E}}} = {180^0}\) (tính chất)

Do đó, \(\widehat {KC{\rm{E}}} = {180^0} - \widehat {KA{\rm{E}}}\)   (1)

+) Ta có bốn điểm AKMB thuộc đường tròn (O) nên tứ giác AKMB nội tiếp

Do đó, \(\widehat {KA{\rm{B}}} + \widehat {KMB} = {180^0}\). Suy ra \(\widehat {KMB} = {180^0} - \widehat {KA{\rm{B}}}\) (2)

+) Từ (1) và (2) ta có: \(\widehat {KC{\rm{E}}} = \widehat {KMB}\) mà \(\widehat {KC{\rm{E}}} = \widehat {MCB}\) (đối đỉnh)

Nên \(\widehat {MCB} = \widehat {KMB}\)

+) Xét \(\Delta BMC\) và \(\Delta BKM\) có:

\(\widehat {MBK}\) chung; \(\widehat {MCB} = \widehat {KMB}\) (cmt)

Nên  (góc-góc)

Do đó \(\frac{{BM}}{{BK}} = \frac{{BC}}{{BM}}\). Suy ra\(B{M^2} = BK \cdot BC\).

c. Xét đường tròn ngoại tiếp tứ giác AECK, ta có:

\(\widehat {EKC} = \widehat {EAC}\) (hai góc nội tiếp cùng chắn cung \[EC\]) (3)

+) Xét tam giác BAI có BK, IE là hai đường cao, mà chúng cắt nhau tại C.

Suy ra C trực tâm tam giác \[BAI\] nên \(\widehat {ADB} = 90^\circ \). Suy ra \[D\] thuộc đường tròn (O)

+) Ta có \(\widehat {CKD} = \widehat {EAC}\) (hai góc nội tiếp cùng chắn cung \[BD\]của đường tròn (O). (4)

Từ (3) và (4) suy ra \(\widehat {EKC} = \widehat {CKD}\)

Do đó, \[KC\] là tia phân giác của góc \[EKD\]

+) Chứng minh tương tự câu a ta được tứ giác \[BECD\]nội tiếp

Suy ra \(\widehat {CDE} = \widehat {CBE}\) (2 góc nội tiếp cùng chắn cung \[CE\])

Mặt khác \(\widehat {KDC} = \widehat {CBE}\) (2 góc nội tiếp cùng chắn cung \[AK\]của\[\left( {\rm{O}} \right)\])

Suy ra \(\widehat {CDE} = \widehat {KDC}\), suy ra \[DC\] là tia phân giác của góc \[KDE\]

Tam giác \[KDE\] có \[C\] là giao điểm của hai đường phân giác góc \[K\] và \[D\]

Suy ra \[C\] cách đều 3 cạnh của tam giác \[KDE\]