a) Rút gọn biểu thức: \(E = 3\sqrt 5 - \sqrt {20} + \sqrt 5 \).
b) Giải phương trình: \({x^2} + 4x + 3 = 0\).
c) Giải hệ phương trình: \(\left\{ \begin{array}{l}3x - y = 3\\2x + y = 7\end{array} \right.\).
Quảng cáo
Trả lời:
Giải bởi Vietjack
a)Rút gọn biểu thức \(E = 3\sqrt 5 - \sqrt {20} + \sqrt 5 \)
.Ta có: \(E = 3\sqrt 5 - \sqrt {4.5} + \sqrt 5 = 3\sqrt 5 - \sqrt 4 .\sqrt 5 + \sqrt 5 \)
.\( = 3\sqrt 5 - 2\sqrt 5 + \sqrt 5 = \left( {3 - 2 + 1} \right)\sqrt 5 = 2\sqrt 5 \).
b)Giải phương trình \({x^2} + 4x + 3 = 0\)
.Ta có: \(a = 1,{\rm{ }}b = 4,{\rm{ }}c = 3;{\rm{ }}a - b + c = 0\)
.Phương trình có nghiệm \({x_1} = - 1\) và \({x_2} = - 3\).
c)Giải hệ phương trình \(\left\{ \begin{array}{l}3x - y = 3\\2x + y = 7\end{array} \right.\)
.Ta có: \(\left\{ \begin{array}{l}3x - y = 3\\2x + y = 7\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}5x = 10\\2x + y = 7\end{array} \right.\)
.\( \Leftrightarrow \left\{ \begin{array}{l}x = 2\\y = 3\end{array} \right.\)
Vậy hệ phương trình có nghiệm duy nhất \(\left( {x;y} \right) = \left( {2;3} \right)\).
Hot: 1000+ Đề thi cuối kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Hình vẽ
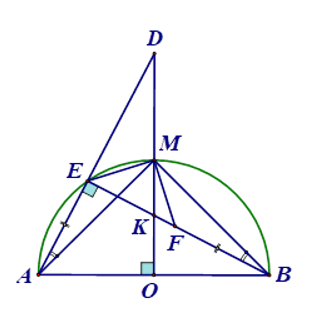
a)Ta có: \(\widehat {AEK} = \widehat {AEB} = 90^\circ \) (góc nội tiếp chắn nửa đường tròn), \(\widehat {AOK} = \widehat {AOM} = 90^\circ \) (\(M\) là điểm chính giữa của cung \(AB\)).
\(\widehat {AEK} + \widehat {AOK} = 180^\circ \) nên \(EAOK\) là tứ giác nội tiếp.
b)Xét \(\Delta AEM\) và \(\Delta BFM\) có:
\(AE = BF\) (giả thiết), \(AM = BM\) (giả thiết), \(\widehat {EAM} = \widehat {MBF}\) (góc nội tiếp cùng chắn cung \(EM\))
\( \Rightarrow \Delta AEM = \Delta BFM\) (c-g-c)\( \Rightarrow EM = FM\)\( \Rightarrow \Delta MEF\) cân tại \(M\)
Mặt khác \(\widehat {MEF} = \widehat {MEB} = \frac{1}{2}\widehat {MOB} = 45^\circ \)
\( \Rightarrow \Delta MEF\) vuông cân tại \(M\).
c)Ta có: \(\widehat {MEF} = 45^\circ \) (\(\Delta MEF\) vuông cân tại \(M\)), mà \(\widehat {KED} = \widehat {KEA} = 90^\circ \)
\( \Rightarrow \widehat {DEM} = 45^\circ \)
\( \Rightarrow EM\) là phân giác của \(\widehat {DEK}\)
\( \Rightarrow \frac{{MK}}{{EK}} = \frac{{MD}}{{ED}}\) (tính chất đường phân giác của tam giác)\( \Rightarrow MK.ED = MD.EK\).
Lời giải
Thể tích của bút chì: \({V_B} = \pi {.4^2}.180 = 2880\pi \left( {m{m^3}} \right)\),
thể tích của lõi chì \({V_C} = \pi {.1^2}.180 = 180\pi \left( {m{m^3}} \right)\)
Thể tích phần gỗ của một chiếc bút chì: \({V_G} = {V_B} - {V_C} = 2700\pi \left( {m{m^3}} \right)\). Thể tích phần gỗ của 2024 chiếc bút chì là: \(V = 2024 \times 2700\pi = 5464800\pi = 17159472\left( {m{m^3}} \right)\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập