Đề thi tuyển sinh vào lớp 10 môn Toán năm 2023-2024 Đắk Lắk có đáp án

a)Cho biểu thức \(A = {\left( {\frac{{\sqrt x }}{2} - \frac{1}{{2\sqrt x }}} \right)^2}.\left( {\frac{{\sqrt x  - 1}}{{\sqrt x  + 1}} + \frac{{\sqrt x  + 1}}{{1 - \sqrt x }}} \right)\) với \(x > 0,x \ne 1\). Rút gọn \(A\)

Ta có: \[A = {\left( {\frac{{x - 1}}{{2\sqrt x }}} \right)^2}.\left( {\frac{{\sqrt x  - 1}}{{\sqrt x  + 1}} - \frac{{\sqrt x  + 1}}{{\sqrt x  - 1}}} \right)\]

\[ = {\left( {\frac{{x - 1}}{{2\sqrt x }}} \right)^2}.\frac{{{{\left( {\sqrt x  - 1} \right)}^2} - {{\left( {\sqrt x  + 1} \right)}^2}}}{{x - 1}}\]

\( = {\left( {\frac{{x - 1}}{{2\sqrt x }}} \right)^2}.\frac{{ - 4\sqrt x }}{{x - 1}}\)

\( = \frac{{1 - x}}{{\sqrt x }}\).

b)Tìm tất cả các giá trị của \(x\) để \(A \ge 0\)

Vì \(x > 0\) nên \(A \ge 0 \Leftrightarrow 1 - x \ge 0 \Leftrightarrow x \le 1\)

a)Ta có: \(\left( d \right){\rm{//}}\left( \Delta  \right) \Leftrightarrow \left\{ \begin{array}{l}4m = 5 - m\\5 \ne  - 3\end{array} \right.\)

\( \Leftrightarrow m = 1\).

Vậy \(m = 1\) thì hai đường thẳng \(\left( d \right)\) và \(\left( \Delta  \right)\) song song với nhau.

b)Phương trình hoành độ giao điểm của \(\left( d \right)\) và \(\left( P \right)\) là:

\({x^2} = 4mx + 5\)\( \Leftrightarrow {x^2} - 4mx - 5 = 0\) (*)

Ta có: \(a = 1,c =  - 5;ac =  - 5 < 0\) nên phương trình (*) luôn có hai nghiệm phân biệt \({x_1},{x_2}\) với mọi giá trị của tham số \(m\).

Theo hệ thức Vi-et ta có \({x_1} + {x_2} = 4m\), vì \({x_2}\) là nghiệm của phương trình (*) nên  \(x_2^2 = 4m{x_2} + 5\).

Ta có: \(x_2^2 + 4m{x_1} = 105 \Leftrightarrow 4m{x_2} + 5 + 4m{x_1} = 105\)

Gọi chiều rộng, chiều dài của hình chữ nhật lần lượt là \(x,y\left( m \right)\), điều kiện \(x > 0,y > 45\). Ta có: \(y - x = 45\) (1)

Chiều dài giảm hai lần, chiều rộng tăng 3 lần ta được hình chữ nhật có hai cạnh là \(\frac{y}{2}\) và \(3x\). Theo giả thiết chu vi không đổi nên: \(2\left( {x + y} \right) = 2\left( {3x + \frac{y}{2}} \right)\) (2)

Từ (1) và (2) ta có hệ phương trình \(\left\{ \begin{array}{l}y - x = 45\\2\left( {x + y} \right) = 2\left( {3x + \frac{y}{2}} \right)\end{array} \right.\)

\( \Leftrightarrow \left\{ \begin{array}{l}x = 15\\y = 60\end{array} \right.\)

Hình vẽ

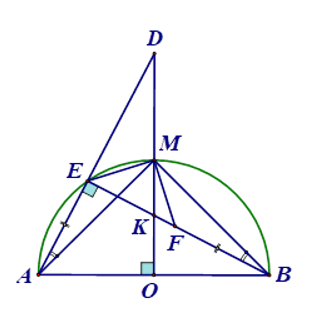
a)Ta có: \(\widehat {AEK} = \widehat {AEB} = 90^\circ \) (góc nội tiếp chắn nửa đường tròn), \(\widehat {AOK} = \widehat {AOM} = 90^\circ \) (\(M\) là điểm chính giữa của cung \(AB\)).

\(\widehat {AEK} + \widehat {AOK} = 180^\circ \) nên \(EAOK\) là tứ giác nội tiếp.

b)Xét \(\Delta AEM\) và \(\Delta BFM\) có:

\(AE = BF\) (giả thiết), \(AM = BM\) (giả thiết), \(\widehat {EAM} = \widehat {MBF}\) (góc nội tiếp cùng chắn cung \(EM\))

\( \Rightarrow \Delta AEM = \Delta BFM\) (c-g-c)\( \Rightarrow EM = FM\)\( \Rightarrow \Delta MEF\) cân tại \(M\)

Mặt khác \(\widehat {MEF} = \widehat {MEB} = \frac{1}{2}\widehat {MOB} = 45^\circ \)

\( \Rightarrow \Delta MEF\) vuông cân tại \(M\).

c)Ta có: \(\widehat {MEF} = 45^\circ \) (\(\Delta MEF\) vuông cân tại \(M\)), mà \(\widehat {KED} = \widehat {KEA} = 90^\circ \)

\( \Rightarrow \widehat {DEM} = 45^\circ \)

\( \Rightarrow EM\) là phân giác của \(\widehat {DEK}\)